Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

Р≈33,56 см
Объяснение:
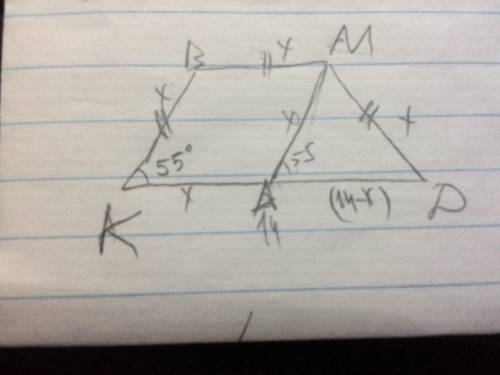
1. Достроим АМ || КВ , следовательно уг ДАМ=уг АКВ=55, тогда МАКВ - параллелограмм
пусть АМ =х=АК=КВ=ВМ=МР, тогда АД=КД-АК=14-х
2. Рассм треуг АМР - равнобед:
угАМД=180-55-55=70град;
по теореме синусов имеем соотношение :
AM:sinMAD=AD:sinAMD
x:sin55=(14-x):sin70
x*sin70=(14-x)*sin55
x*sin70+x*sin55=14*sin55
x(sin70+sin55)=14*sin55
x=14*sin55:(sin70+sin55)
x≈14*0,82:(0,94+0,82)
x≈6,52 см
3. Ртрапеции= 14+3х≈14+3*6,52≈33,56 см
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid
17:25= 124 124·28=323 ответ: 323 см