▪︎58 - В)
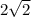
▪︎59 - С)
Объяснение:
▪︎58.
Две хорды проведенные из одной точки окружности взаимно перпендикулярны составляют вписанный угол 90° => этот угол опирается на дугу 180° и центральный угол который опирается на эту же дугу равен 180° => он является диаметром.
Получаем прямоугольный треугольник, где диаметр - гипотенуза, а хорды - катеты. По т. Пифагора:
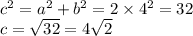
следовательно радиус равен половине диаметра:
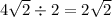
▪︎59.
Объяснение то же самое: две взаимно перпендикулярные хорды проведенные из одной точки окружности являются вписанным углом, который равен 90° => этот угол опирается на дугу равную 180° и соответсвенно центральный угол также опирается на эту же дугу и он является диаметром и гипотенузой.
А если радиус 6 см то диаметр 12 см, а по т.Пифагора:
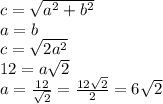
30
Объяснение:
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и ОН⊥CD.
ОК = 15, ОН = 8 - расстояния от центра до хорд АВ и CD соответственно.
ΔАОВ равнобедренный, значит ОК - высота и медиана.
АК = КВ = 1/2АВ = 8
Из прямоугольного треугольника АОК по теореме Пифагора:
ОА = √(AK² + OK²) = √(8² + 15²) = √(64 + 225) = √289 = 17
ОС = ОА = 17
Из прямоугольного треугольника СОН по теореме Пифагора:
СН = √(CO² - OH²) = √(17² - 8²) = √(289 - 64) = √225 = 15
ΔOCD равнобедренный, значит ОН - высота и медиана.
CD = 2CH = 2 · 15 = 30