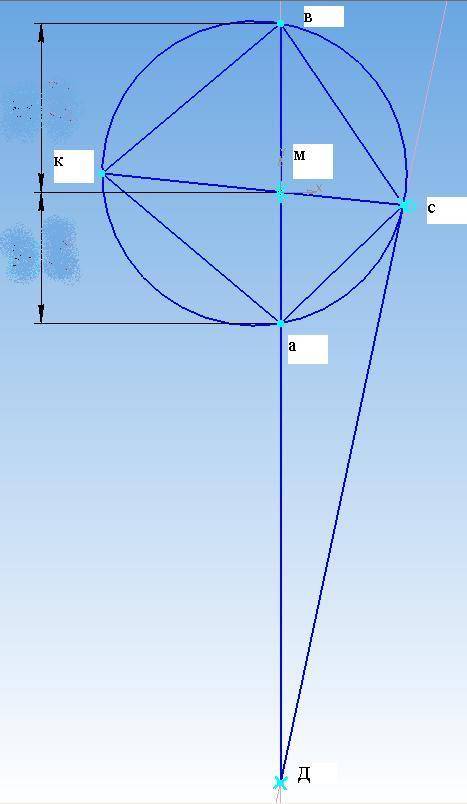
Высоты АА1 и СС1 остроугольного треугольника АВС пересекаются в точке Е. Докажите что углы CC1A1 и СAA1 равны.
Доказательство через вписанные углы в описанной окружности.
Т.к. в прямоугольных треугольниках АС1С и АА1С общая гипотенуза, то вокруг них можно описать общую окружность. В ней вписанные углы CC1A1 и СAA1 опираются на дугу, стягиваемую общей для них хордой. Вписанные углы, опирающиеся на одну дугу, равны, что и требовалось доказать.
∆ АЕС1 и ∆ СЕА1 - прямоугольные и имеют равные вертикальные углы при Е. - Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
Отношения катетов, противолежащих равным углам подобных треугольников, к гипотенузе - равны ( это отношение - синусы равных углов).⇒
ЕС1:ЕА=ЕА1:ЕС.
Рассмотрим ∆ ЕАС и ∆ ЕА1С1. Они имеют равные вертикальные углы при Е, а их стороны. содержащие равные углы, пропорциональны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны. то такие треугольники подобны.
Следовательно, ∆ЕАС и ∆ ЕА1С1 подобны.
Углы ЕАС и ЕС1А1 лежат напротив сходственных сторон, следовательно, равны, ч.т.д

100 см, 100 см, 20 см.
Объяснение:
Пусть ВС=АС=х см, тогда АВ=х/5 см.
х+х+х/5=220
5х+5х+х=1100
11х=1100
х=100
ВС=АС=100 см, АВ=100:5=20 см.