
Объяснение:
Вариант 1
Часть А
1
S=1/2×a×h
a=5+3=8
h=6
S=1/2×8×6=24
ответ : 1) 24
Часть В
2
а=12 см
b=5 см
d=корень (а^2+b^2)=корень (12^2+5^2)=
=корень 169=13 см
Часть С
3
Боковая сторона b=15 cм
Высота h=9 cм
Основание а=?
а/2=корень (b^2-h^2)=корень (15^2-9^2)=
=корень144=12 см
а=12×2=24 см
4
S=(a+b)/2×h
a=17 cм
b=5 cм
c=10 cм
Х=(а-b) /2=(17-5)/2=6 cм
h=корень (с^2-Х^2)=корень (10^2-6^2)=
=корень 64=8 см
S=(17+5)/2×8=88 cм^2
5
AB=CD=x
BC=AD=3x
ВD^2=AB^2+AD^2
20^2=x^2+(3x)^2
400=x^2+9x^2
400=10x^2
X^2=40
X=корень40
АВ=СD=корень 40
ВС=АD=3корень40
S=1/2×AD×AB=1/2×3 корень40×корень40=
=1/2×3×40=60
S=1/2×BD×AH
2S=BD×AH
AH=2S/BD
AH=2×60/20=6
ответ : 6
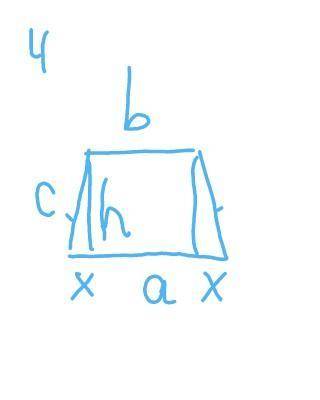
Рассмотрим 2 треугольника: АВВ1, АОС1:
- оба прямоугольные
- уголВАО общий
известно, что сумма острых углов прямоугольного треугольника величина постоянная (равна π/2), или:
уголАВВ1+уголВАВ1=уголАОС1+уголС1АО(=π/2),
очевидно: уголВАВ1≡уголС1АО(≡ВАО), уголАВВ1≡уголАВС, уголАОС1≡уголАОС⇒получаем:
уголАВС+уголВАО=уголАОС+уголВАО,
уголАВС=уголАОС, ч.т.д
или вот так:
уголВСС1=уголОСВ1 (вертикальные при пересекающихся ОС1иВВ1))
Тогда π/2-уголВСС1=π/2-уголОСВ1,
а из треугольников(прямоугольных) ΔВСС1, ΔОСВ1 получим, что эти углы равны тем которые нам надо сравнить:
уголАВС=уголАОС, ч.т.д
2) это утверждение верно, только если АС=СВ, то есть нам дан равнобедренный тупоугольный треугольник.