
1)Сначала рассмотрим треугольники АВО и СОМ
АО = ОС - по условию
ВО = ОМ - по условию
угол ВОА = угол МОС - вертикальные, следовательно треугольники равны по первому признаку равенства треугольников, следовательно АВ = СМ и угол АВО = углу СМО
2)Затем рассмотрим треугольники ВОС и АОМ
ВО = ОМ - по условию
ОС = ОА - поу словию
угол ВОС = углу АОМ - вертикальные, следовательно треугольники равны по первому признаку равенства треугольников, следовательно ВС = АМ и угол АМО = угол ОВС
3) угол АВС = угол АВО + угол ОВС
угол АМС = угол АМО + угол ОМС
угол АМО = угол ОВС
угол АВО = углу СМО, следовательно угол АВС = углу АМС
4)Рассмотрим треугольники АВС и АМС
АВ = СМ - по доказонному (1)
ВС = АМ - по доказонному (2)
угол АВС = углу АМС - по доказонному (3), следовательно треугольники равны по первому признаку равенства треугольников
Можно найти площадь методом нахождения площади всех фигур, при этом прибавив их
Площадь прямоугольника с сторонами 5 и 1 = 5 ед.²
Опустим высоту с стороны прямоугольника длиной 1 ед. Она будет равняться 2, так как высота будет параллельна с высотой слева. У нас получился ещё один прямоугольник с сторонами 5 и 2. Его площадь равна 10 ед.² (если что, для площади прямоугольника мы умножаем стороны)
У нас также появился треугольник с сторонами 2 и (9-5) = 4. Найдём площадь данного треугольника: 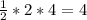 ед.²
ед.²
Треугольник слева будет равен треугольнику, который мы создали, так что его площади тоже равна 4 ед.²
Прибавляем все значения. Это равняется 23 ед.²
1)
2).
Объяснение:
1).
уравнение сферы с центром в точке А (х0;у0;z0) и радиусом r
выделим полные квадраты при переменных:
- уравнение сферы с центром в точке А (-1;1;0) и радиусом r=2
2).
- уравнение сферы с центром в точке А (1;0; -1) и радиусом r=3