3. В параллелограмме со сторонами 10 см и 14 см на меньшую сторону опущена высота, длиной 7 см. Найдите длину высоты, опущенную на большую сторону.

👇

Увидеть ответ

Открыть все ответы

Ответ:

Dasha29081

17.05.2021

сторони трикутника відносяться як 5: 6: 7, а периметр=36см

нехай х- коефіцієнт пропорційності, тоді

5х+6х+7х=36см

х=2см

тоді сторони даного трикутника:

5*2см=10см

6*2см=12см

7*2см=14см

за властивістю середньої лінії трикутника, що сполучає середини двох його сторін та дорівнює половині третьої сторони:

10см: 2=5см,

12см: 2=6см,

14см: 2=7см

5см,6см, 7см - сторони трикутника, вершини якого є середини сторін даного трикутника, відповідно його периметр

5см+6см+7см=18см

відповідь: 5см, 6см, 7см - сторони;

18см - периметр.

4,6(60 оценок)

Ответ:

Ksenon102

17.05.2021

1. Найти угол между векторами AС и АB.

$\overrightarrow{AC}=(1-1;\;2-3;\;1-0)=(0;\;-1;\;1)\\ \\ \overrightarrow{AB}=(2-1;\;3-3;\;1-0)=(1;\;0;\;1)$

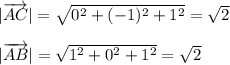
$|\overrightarrow{AC}|=\sqrt{0^2+(-1)^2+1^2} =\sqrt{2} \\ \\|\overrightarrow{AB}|=\sqrt{1^2+0^2+1^2} =\sqrt{2}$

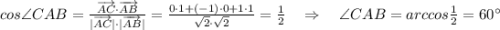
$cos\angle CAB=\frac{\overrightarrow{AC}\cdot\overrightarrow{AB}}{|\overrightarrow{AC}|\cdot|\overrightarrow{AB}|}=\frac{0\cdot1+(-1)\cdot0+1\cdot1}{\sqrt{2}\cdot \sqrt{2} } =\frac{1}{2} \quad \Rightarrow\quad \angle CAB=arccos\frac{1}{2}=60^{\circ}$

*Можно искать не косинус угла, а найти длину вектора BC, тогда ΔABC -- равносторонний и углы равны по 60°.

2. Найти координаты центра сферы и длину ее радиуса. Найти значение m.

Приведём уравнение к общему виду (x - x₀)² + (y - y₀)² + (z - z₀)² = R²:

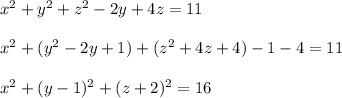
$x^2+y^2+z^2-2y+4z=11\\ \\ x^2+(y^2-2y+1)+(z^2+4z+4)-1-4=11\\ \\ x^2+(y-1)^2+(z+2)^2=16$

Тогда O (x₀; y₀; z₀) -- центр сферы, O (0; 1; -2),

R² = 16 ⇒ R = 4

Если точка принадлежит сфере, то подставив её координаты в уравнение, получится верное равенство. Подставим точки A и B в уравнение сферы:

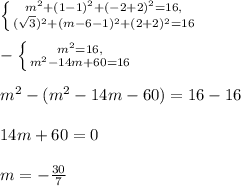
$\left \{ {{m^2+(1-1)^2+(-2+2)^2=16,} \atop {(\sqrt{3} )^2+(m-6-1)^2+(2+2)^2=16}} \right. \\ \\ -\left \{ {{m^2=16,} \atop {m^2-14m+60=16}} \right. \\ \\ m^2- (m^2-14m-60)=16-16\\ \\ 14m+60=0\\ \\ m=-\frac{30}{7}$

3. Найти уравнение плоскости α.

Ax + By + Cy + D = 0 -- общее уравнение плоскости.

n = (A; B; C) -- вектор нормали ⇒ A = 1, B = 2, C = 3, тогда

$\alpha:\;\; x + 2y+ 3z + D = 0$

Если точка принадлежит плоскости, то подставив её координаты в уравнение, получится верное равенство:

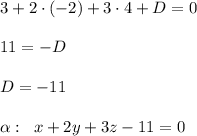
$3 + 2\cdot(-2)+ 3\cdot 4 + D = 0\\ \\ 11 =-D\\ \\ D=-11\\ \\ \alpha :\;\;x+2y+3z-11=0$

4. Найти общее уравнение прямой.

Общее уравнение прямой представляет собой систему уравнений двух пересекающихся плоскостей. Решение этой системы есть пересечение плоскостей, то есть прямая.

Зададим прямую параметрически:

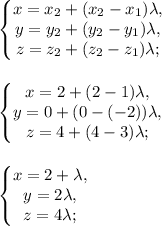
$\left\{\begin{matrix}x=x_2+(x_2-x_1)\lambda,\\ y=y_2+(y_2-y_1)\lambda,\\ z=z_2+(z_2-z_1)\lambda;\end{matrix}\right\\\\\\ \left\{\begin{matrix}x=2+(2-1)\lambda,\\ y=0+(0-(-2))\lambda,\\ z=4+(4-3)\lambda;\end{matrix}\right\\\\\\ \left\{\begin{matrix}x=2+\lambda,\\ y=2\lambda,\\ z=4\lambda;\end{matrix}\right$

Исключим параметр λ:

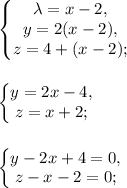
$\left\{\begin{matrix}\lambda=x-2,\\ y=2(x-2),\\ z=4+(x-2);\end{matrix}\right\\\\ \\ \left\{\begin{matrix}y=2x-4,\\ z=x+2;\end{matrix}\right\\ \\\\\ \left\{\begin{matrix}y-2x+4=0,\\ z-x-2=0;\end{matrix}\right$