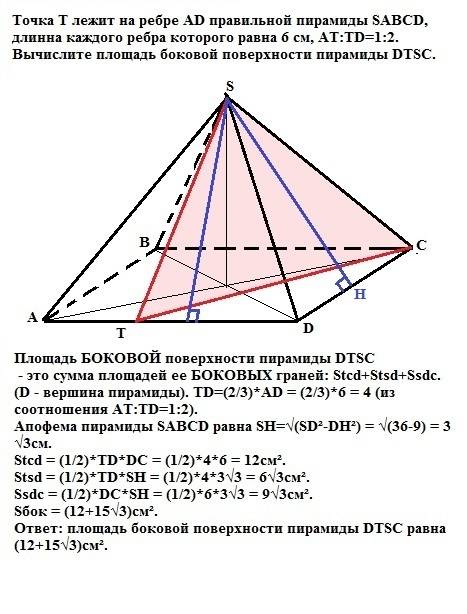
Пирамида SABCD правильная, значит в основании ее лежит квадрат, а боковые грани - равносторонние треугольники со стороной = 6 (дано). Апофема пирамиды SABCD (высота ее боковых граней) равна SH=√(SD²-DH²) = √(36-9) = 3√3см.
Площадь БОКОВОЙ поверхности пирамиды DTSC - это сумма площадей ее БОКОВЫХ граней: Stcd+Stsd+Ssdc. (D - вершина этой пирамиды). TD=(2/3)*AD = (2/3)*6 = 4 (из соотношения AT:TD=1:2).
Stcd = (1/2)*TD*DC = (1/2)*4*6 = 12см².
Stsd = (1/2)*TD*SH = (1/2)*4*3√3 = 6√3см².
Ssdc = (1/2)*DC*SH = (1/2)*6*3√3 = 9√3см².
Sбок = (12+15√3)см².
ответ: площадь боковой поверхности пирамиды DTSC равна
Sdtsc=(12+15√3)см².
V=Sоснh=a²h, где a-сторона основания пирамиды, h- ее высота
Sбок=PL=4al, где l-длина пирамиды, P-периметр
Sбок=Ph=4ah
Sбок.сеч=ah√2=al√2
Sперп.сечения=a²
По поводу выразить формулу через d. Лучше всего приведу пример: В правильной четырёхугольной призме площадь основания 144 см2, а высота 14 см. Найти диагональ призмы и площадь полной поверхности.
Решение: Правильный четырехугольник - это квадрат. a=√144 = 12 см. dпрямоуг.призмы=√( 12² + 12² ) = √288 = 12√2
и диагональ правильной призме будет равна dправ.призмы=√( ( 12√2 ² + 14² ) = 22 см
ответ : 22 см
Я думаю сейчас будет более понятно
смотрим рисунок во вложении
та как треугольники ВСС1 и ВСВ1 - прямоугольные, то их можно описать окружностью, диаметр которой совпадает с общей гипотенузой ВС
угол ВС1В1 и угол ВСВ1 - опираются на одну и ту же дугу окружности
значит угол ВС1В1 и угол ВСВ1 - равны а значит угол АС1В1 и угол ВСА - равны
угол С1В1С и угол С1ВС - опираются на одну и ту же дугу окружности
значит угол С1В1С и угол С1ВС - равны а значит угол С1В1А и угол АВС - равны
так как угол АС1В1 и угол ВСА - равны
так как угол С1В1А и угол АВС - равны
так как угол ВАС и угол В1АС1 - равны
то треугольники АВС и АВ1С1 - подобны - доказано