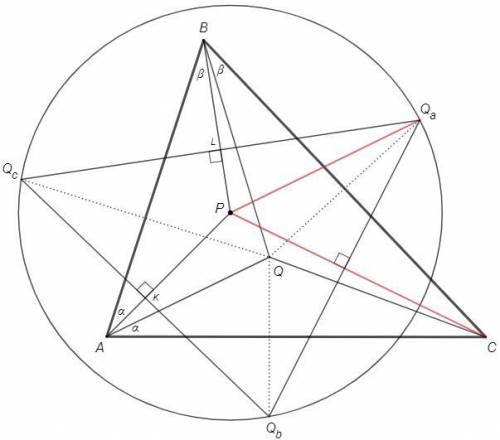
Свойство изогоналей:
AP и AQ - изогонали угла
Qb и Qc симметричны Q относительно сторон угла
Тогда AP - серединный перпендикуляр к QbQc
И тогда P - центр описанной окружности △QaQbQc
В четырехугольнике PKQcL противоположные углы прямые, следовательно сумма двух других также 180.
APB +Qc =180
Qc =QaPQb/2 (вписанный равен половине центрального)
CPQa =QaPQb/2 (CP - серединный перпендикуляр к QaQb)
=> CPQa =180-APB
a +b +APB =180 (△APB)
AQB = a +ACQ +b +BCQ = a +b +C (сумма внешних углов △AQC и △BQC)
=> AQB-C =180-APB
CPQa =AQB-C =100-47 =53°
Максимальный из углов равен 122°
Объяснение:
Найдите больший из углов, образованных при пересечении биссектрисы острого угла прямоугольного треугольника и противоположного катета, если второй острый угол треугольника равен 26 °.
Дано:
ΔАВС : ∠С = 90°; ∠А = 26°
BM - биссектриса ∠В; М = ВМ∩АС
Найти:
Наибольший из двух углов ∠ВМА или ∠ВМС
По свойству углов треугольника АВС
∠В = 90° - ∠А = 90° - 26° = 64°
Биссектриса ВМ угла В делит треугольник АВС на два треугольника
ΔВСМ и ΔВМА
ΔВСМ: ∠С = 90° ∠СВМ = 32° (так как ВМ - биссектриса ∠В), тогда
∠ВМС = 90° - 32° = 58°
ΔВМА: ∠А = 26°: ∠АВМ = 32° (так как ВМ - биссектриса ∠В), тогда
∠ВМА = 180° - (26° + 32°) = 122°
Очевидно, что угол ВМА - максимальный угол, он больше ∠ВМС