Как на рисунке ниже добавь линии грани треугольников, а дальше просто, 180гр - сумма всех углов треугольников, а в тр.ОСБ входит прямоугольник ОДБ. ответ 30 гр.
Дорисуй на рисунке углы: который дан и который нужно найти, ОСБ = равнобедренный треугольник, так как ОС и ОБ радиус, от сюда можно сделать вывод что угол ОСБ=СБА= 60 гр и дальше угол СОБ = 180 - 60 - 60 = 60. Дальше, треугольник ОДБ прямоугольный, значит угол ОБД = 180- 60 - 90 = 30, а так как этот треугольник был образован на хорде которую поделили пополам - угол ОАБ = ОБД= 30
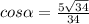
Объяснение:
Дано: Окр.OR-описанная
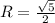
ΔАВС - прямоугольный
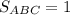
ВК и СМ - медианы
Найти: cosα
1. Окр. OR - описана около ΔАВС ⇒СВ - диаметр (прямой угол опирается на диаметр)
2. Рассмотрим ΔАВС - прямоугольный.
Пусть меньший катет = a, больший - b.
Тогда:
Площадь треугольника:
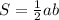
По теореме Пифагора:
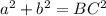
Составим систему:
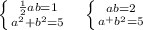
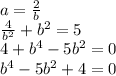
По теореме Виета:
Или
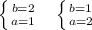
Тогда АС=1; АВ=2.
3. Рассмотрим ΔАВК - прямоугольный.
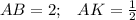(ВК-медиана)
По т. Пифагора
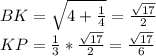(св-во пересекающихся медиан)
4. Рассмотрим Δ МАС - прямоугольный.
(СМ-медиана)
По т. Пифагора
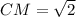
(св-во пересекающихся медиан)
5. Рассмотрим ΔКРС
Используем теорему косинусов:
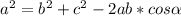
Имеем
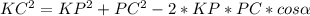
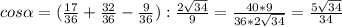
Проведем СН⊥AD, СН - проекция ВН на плоскость (ACD), значит
ВН⊥AD по теореме о трех перпендикулярах.
ΔВАС: ∠ВСА = 90°,
cos∠β = AC / AB
ΔBAH: ∠BHA = 90°,
cos∠α = AH / AB ⇒ AB = AH / cos∠α
ΔAHC: ∠AHC = 90°,
cos∠γ = AH / AC ⇒ AC = AH / cos∠γ
cos∠β = (AH / cos∠γ) / (AH / cos∠α) = cos∠α / cos∠γ
cos∠β = cos 60° / cos 30° = 1/2 / (√3/2) = 1/√3
∠BAC = arccos(1/√3)
Здесь доказана теорема о трех косинусах:
Косинус угла между наклонной и прямой, лежащей в плоскости, равен произведению косинуса угла между наклонной и плоскостью на косинус угла между проекцией и этой прямой.
cosα = cosβ · cosγ