Відповідь:
5400 см^2.
Пояснення:
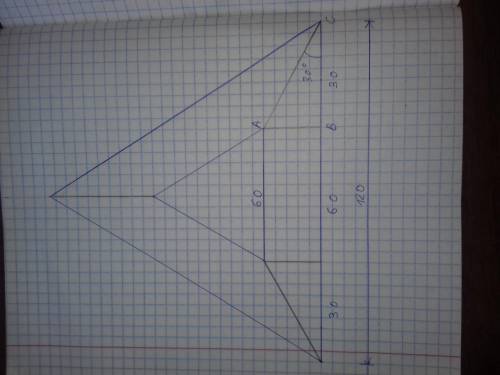
Боковые грани правильной усеченной треугольной пирамиды - это трапеции с основаниями 60 см. и 120 см. Найдем высоту трапеции.
Рассмотрим вид сверху на пирамиду.
Треугольник АВС имеет угол В - прямой, угол С = 30° и сторону ВС = 30 см.
АВ = 30 × tg 30° = 17,32 см.
Если посмотреть на пирамиду сбоку, то высота пирамиды и отрезок АВ - это катеты треугольника, гипотенузой которого является высота трапеции ( боковой грани усеченной пирамиды ).
Н = sqrt ( 10^2 × 17,32^2 ) = sqrt 400 = 20 см.
Вычислим площадь боковой грани
Sтр = ( 60 + 120 ) / 2 × 20 = 1800 см^2.
Площадь боковой поверхности нашей пирамиды равна трем площадям трапеции.
S = 3 × Sтр = 3 × 1800 = 5400 см^2.
Расстояние от прямой DC до плоскости α - это перпендикуляр из любой точки этой прямой на плоскость α.
Итак, в прямоугольном треугольнике АЕD катет АЕ равен по Пифагору
АЕ=√(AD²-DE²)=√(36²-18²)=18√3.
Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. То есть угол между плоскостью α и плоскостью квадрата - это угол EAD, cинус которого равен отношению противолежащего катета к гипотенузе: Sinβ=ED/AD=18/36=1/2. Значит угол между плоскостями равен 30°.
Площадь проекции квадрата на плоскость α - это площадь прямоугольника AEFB, равная S=AB*AE=36*18√3=648√3см²