
Даны координаты вершин треугольника АВС: А(0;-10),В(-12;-1),С(4;12).Найти:
1. Длину стороны АВ:
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √225 = 15.
2. Уравнение сторон АВ и АС:
АВ : Х-Ха = У-Уа х = у + 10
Хв-Ха Ув-Уа -12 9
9х = -12у -120 сократим на 3 и перенесём налево:
3х + 4у + 40 = 0.
у(АВ) = -0,75х - 10.
АС : Х-Ха = У-Уа
Хс-Ха Ус-Уа
11Х - 2У - 20 = 0
у = 5,5х - 10
3. Величину угла А:
cos A= АВ²+АС²-ВС² = 0,4472136.
2*АВ*АС
A = 1,107149 радиан.
A = 63,434949 градусов.
4. Уравнение высоты CD и ее длину.
к(СД) = -1/к(АВ) = -1/(-0,75) = 4/3.
у = (4/3)х + в. Для определения "в" подставим координаты точки С:
12 = (4/3)*4 + в, в = 12 - (16/3) = 20/3.
Уравнение СД: у = (4/3)х + (20/3).
Длину СД можно определить двумя СД = 2S/AB и по координатам точек С и Д.
Приравниваем уравнения АВ и СД: -0,75х - 10 = (4/3)х + (20/3),
(-25/12)х = (20/3) + 10 = 50/3,
х = (50/3)/(-25/12) = (-600/75) = -8,
у = (-3/4)*(-8) - 10 = 6 - 10 = -4. Точка D: (-8; -4).
Длина СД = √((-8-4)² + (-4-12)²) = √(144 + 256) = √400 = 20.
5. Уравнение медианы ВЕ.
Точка Е как середина АС: (2; 1).
ВЕ: Х-Хв = У-Ув х + 12 = у + 1
Хе-Хв Уе-Ув 14 2
Знаменатели сократим на 2: х + 12 = 7у + 7.
Общее уравнение ВЕ: х - 7у + 5 = 0,
с угловым коэффициентом: у = (1/7)х + (5/7).
6. Координаты точки К пересечения медианы ВЕ и высоты CD.
(1/7)х + (5/7) = (4/3)х + (20/3),
(-25/21)х = (125/21)
х = -125/25 = -5, у = (1/7)*(-5) + (5/7) = 0. Точка К:(-5; 0).
7. Уравнение прямой КР, проходящей через точку К параллельно стороне АВ.
Угловой коэффициент равен -0,75.
Уравнение КР: у = (-0,75)х + в. Подставим координаты точки К(-5; 0):
0 = (-0,75)*(-5) + в, в = - (15/4) = -3,75.
у = (-0,75)х - 3,75.
8. Координаты точки М, расположенной симметрично точке А относительно прямой CD.
Так как CD - перпендикуляр к прямой АВ, то точка D(-8; -4) - это та точка, относительно которой требуется найти точку, симметричной точке А.
xM = 2xD - xA = 2*(-8) - 0 = -16,
yM =2yD - yA = 2*(-4) - (-10) = -8 + 10 = 2.
Точка М(-16, 2).
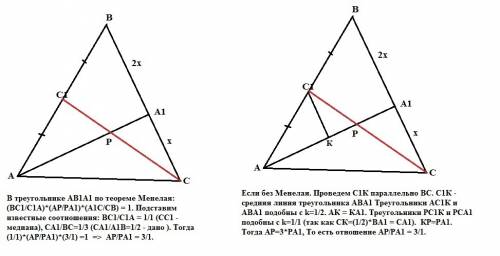
В треугольнике АВ1А1 по теореме Менелая:
(ВС1/С1А)*(АР/РА1)*(А1С/СВ) = 1. Подставим известные соотношения: ВС1/С1А = 1/1 (СС1 - медиана), СА1/ВС=1/3 (СА1/А1В=1/2 - дано ). Тогда (1/1)*(АР/РА1)*(3/1) =1 => АР/РА1 = 3/1.
ответ: медиана СС1 делит отрезок АА1 в отношении АР:РА1 = 3:1.
Без применения формулы Менелая.
Проведем С1К параллельно ВС. С1К - средняя линия треугольника АВА1, так как точка С1 делит сторону АВ пополам, а отрезок КС1 параллелен стороне ВС по построению. Треугольники АС1К и АВА1 подобны с коэффициентом k=1/2. АК=КА1. Треугольники РС1К и РСА1 подобны с коэффициентом k=1/1 (то есть равны, так как СК=(1/2)*ВА1). КР=РА1.Тогда АР = 3*РА1. То есть отношение АР/РА1 = 3:1.
Треугольники равны по первому признаку равенства треугольников, ВО=OD, AO=OC, угол АОВ=углу СОД(вертикальные углы)