
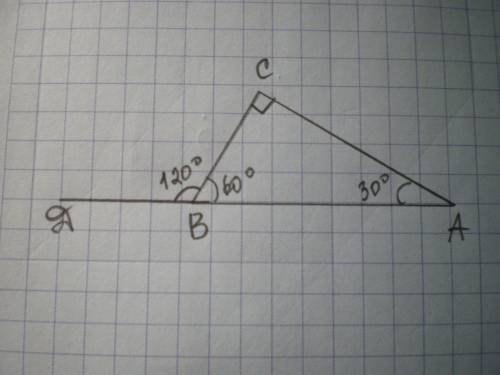
Дано: ΔАВС - прямоугольный, ∠С=90°, ∠ДВС=120°, АВ+ВС=24 см.
Найти АВ, ВС.
По свойству смежных углов ∠ДВА+∠СВА=180°, тогда
∠СВА=180-∠ДВС=180-120=60°.
По свойству острых углов прямоугольного треугольника
∠А=90-∠СВА=90-69=30°
В треугольнике против большей стороны лежит больший угол, поэтому АВ - большая сторона. Против меньшей стороны лежит меньший угол, поэтому ВС - меньшая сторона.
ВС=1\2 АВ по свойству катета, лежащего против угла 30°.
Составим уравнение: АВ+1\2 АВ = 24; 1,5 АВ = 24; АВ=16 см.
ВС=16:2=8 см.
ответ: 8 см, 16 см.
точка В есть вершиной треугольника АВС. Он равнобедренной , где АВ = ВС= 10
Соеденим т.О с точкой В. ВО пересеклось с основанием АС в точке К. Где ВК есть высотой треугольника.
ВК перпендикулярна до АС.
Рассмотрим треугольник АВК, где угол ВКА - прямой = 90градусов.
За теоремой Пифагора находим ВК:
ВК^2 = AB^2 - AK^2, где АК = 16 / 2 = 8. Потому что ВК также есть и медианой.
ВК^2 = 100 - 64 =36
ВК = 6
R - радиус описанной окружности.
R = АВ^2 / (2 * ВК) = 100 / 12 = 25/3 = 8целых и 1/3.