ответ: 676π.
Объяснение:
Сечение шара - круг. Площадь круга: S = πr².
S₁ = πr₁² = 25π ⇒ r₁ = 5
S₂ = πr₂² = 144π ⇒ r₂ = 12
Отрезок, соединяющий центр шара с центром сечения, перпендикулярен сечению.
Обозначим ОС = х, тогда OS = 17 - х.
Из прямоугольных треугольников ОСА и OSB выразим радиус шара по теореме Пифагора:
R² = (17 - x)² + r₁² = (17 - x)² + 25
R² = x² + r₂² = x² + 144
(17 - x)² + 25 = x² + 144
289 - 34x + x² + 25 = x² + 144
34x = 170
x = 5
R = √(x² + 144) = √(25 + 144) = √169 = 13
Sпов. шара = 4πR² = 4 · π · 169 = 676π
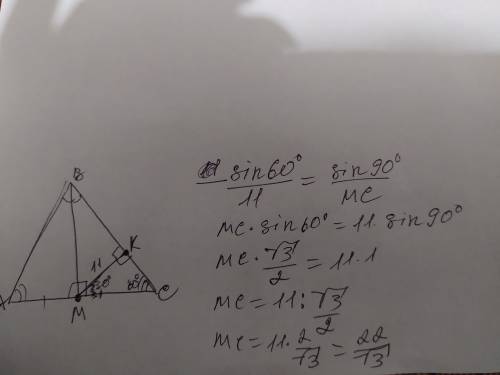
ответ: ВМ=22
Объяснение: обозначим прямую от точки М до стороны ВС - МК=11 высотой стороны ВС. У нас получился прямоугольный треугольник МСК, в котором угол С =60°(по условиям, поскольку ∆АВС равносторонний). В ∆МСК угол СМК=30°(180-90-60). Теперь применим теорему синусов и найдём сторону МС: теорема синусов на фото ниже
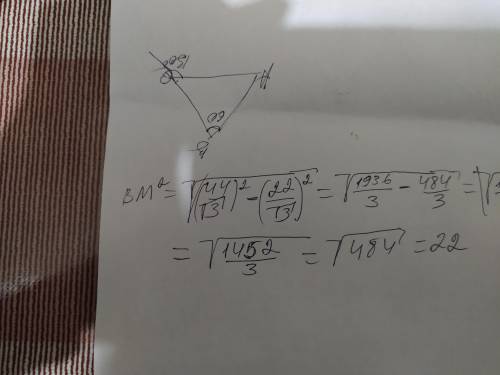
В ∆СВМ угол СВМ=30°(по условиям, поскольку медиана проведённая из вершины В является ещё биссектрисой, которая делит угол пополам и высотой. В прямоугольном ∆СВМ сторона ВС=22/√3×2=44√3(по свойствам угла 30°- катет, лежащий напротив угла 30°=половине гипотенузы). Теперь по теореме Пифагора ВМ= решение по теореме Пифагора на фото ниже