16 см, 30 см.
Объяснение:
Нехай катет а=8х см, в=15х см, тоді за теоремою Піфагора
с²=а²+в²; 34²=(8х²)+(15х)²; 1156=64х²+225х²; 289х²=1156; х²=4; х=2.
а=8*2=16 см; в=15*2=30 см.
Пусть катеты равны а и b, гипотенуза равна с и высота, проведённая из вершины прямого угла, равна h.
Высота прямоугольного треугольника, проведённая из вершина прямого угла к гипотенузе, равна произведению катетов, делённому на гипотенузу прямоугольного треугольника.Гипотенузу треугольника найдём по теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы) :
c² = a² + b² = 5² + 12² = 25 + 144 = 169
c = √c² = √169 = 13 см.
Тогда, по выше сказанному, h равно :
h = ab / c = 5 см*12 см / 13 см = 60 см²/13 см = 4 8/13 см.
4 8/13 см.
Объяснение:
Из условия нам известно, что ∠DOC равен пяти углам COB.
Если посмотреть на чертеж, то мы увидим, что ∠DOC и ∠COB смежные, а следовательно, их сумма равна 180°. Для нахождения углов DOC и COB составим линейное уравнение:
Пусть x - ∠DOC, тогда ∠COB - 5x. (угол COB равен 5x, т.к. он в 5 раз больше угла DOC)
Получаем:
x + 5x = 180°
6x = 180°
x = 30° (Это мы нашли x, то есть ∠DOC)
∠COB = 30° * 5 = 150°.
Ну а дальше - дело техники.
∠COD = ∠BOA = 150°(все вертикальные углы равны)
∠BOC = ∠AOD = 30°(все вертикальные углы равны).
Задача решена.
Відповідь:
16 і 30 см
Пояснення:
Оскільки в нас є відношення катетів як 8:15, то можемо позначити менший катет 8х, а більший — 15х, тоді відношення буде збережено.
Скористаємося теоремою Піфагора — квадрат гіпотенузи дорівнює сумі квадратів катетів (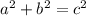 , де a i b — катети, с — гіпотенуза).
, де a i b — катети, с — гіпотенуза).
Тоді отримаємо таке рівняння:
Так як ми позначали за х довжину, а довжина не може бути від'ємна, то нам підходить тільки відповідь х=2.
Отже, довжина меншого катета 8х=8*2=16 см, а більшого — 15х=15*2=30 см.