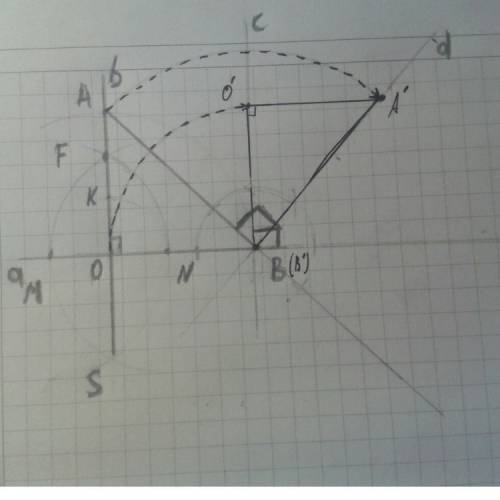
Расстояние от точки до прямой - длина отрезка, проведенная к ней из этой точки перпендикулярно.
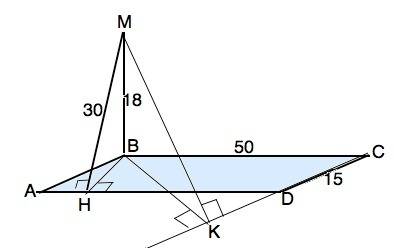
МВ перпендикулярна плоскости параллелограмма, следовательно, любой прямой, проходящей через её основание.
Расстояние от М до AD - наклонная МН. Её проекция ВН⊥AD по т. о 3-х перпендикулярах ⇒ ВН - высота параллелограмма.
∆ МВН - прямоугольный. По т.Пифагора
BH=√(MH²-MB²)=√(900-324)=24 см
S ABCD=BH•AD=24•50=1200 см²
Высота ВК параллелограмма из его площади:
ВК=1200:15=80 см
По т. о 3-х перпендикулярах КМ ⊥ CD, является расстоянием от М до СD - меньшей стороны параллелограмма.
∆ МВК - прямоугольный.
По т.Пифагора
МК=√(MB²+BK²)=√(324+6400)=82 см – это ответ.
.
В прямоугольном треугольнике
катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Поэтому TR=√( RS*RM),
12^2=13* RM, RM=144/13=11 1/13.
MS= 13-144/13=25/13
В прямоугольном треугольнике
высота, проведённая к гипотенуза,есть среднее пропорциональное между отрезками на которые делится гипотенуза:
х=√(144/13*2513) =12*5/13=60/13=
=2 8/13( ед).
.
∆ MST~∆ TSR по двум углам :< S - общий, <TMS=<RTS=90° . В подобных треугольниках сходственные стороны пропорциональны : x/ TR=TS/ RS,
x=(12*5) /13=60/13=4 8/13 (ед).