Щоб знайти радіус кола, описаного навколо правильного дев'ятикутника, можна скористатися формулою:
r = a/ (2 sin(π/n))
де a - довжина сторони дев'ятикутника, n - кількість сторін дев'ятикутника, r - радіус кола, описаного навколо дев'ятикутника.
У даному випадку, довжина сторони дев'ятикутника дорівнює 8 см, і кількість сторін дев'ятикутника дорівнює 9, оскільки дев'ятикутник є правильним. Тоді ми можемо підставити відповідні значення до формули і отримати:
r = 8 / (2 sin(π/9))
Значення sin(π/9) можна знайти, використовуючи тригонометричні таблиці або калькулятор з функцією sin. Підставляючи числове значення, ми отримуємо:
r = 8 / (2 sin(π/9)) ≈ 8 / 1.93 ≈ 4.14
Отже, радіус кола, описаного навколо правильного дев'ятикутника сторона якого дорівнює 8 см, приблизно дорівнює 4.14 см (округлено до двох знаків після коми).
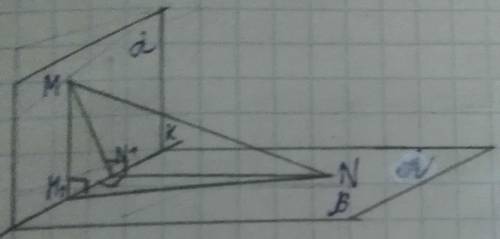
Дано:
α⊥β α∩β = k MN₁⊥NN₁
MM₁⊥k NN₁⊥k MM₁⊥M₁N
MM₁ = 18 см NN₁ = 11 см MN = 25 см
--------------------------------------------------------
Найти:
M₁N₁ - ?
1) ΔMM₁N - прямоугольный (NM₁⊥k, ∠MM₁N = 90°), следовательно используем по теореме Пифагора:
MN² = MM₁² + M₁N² ⇒ M₁N = √MN² - MM₁²
M₁N = √(25 см)² - (18 см)² = √625 см² - 324 см² = √301 см² = √301 см
2) Рассмотрим ΔM₁N₁N:
MM₁⊥k, и NN₁⊥k ⇒ NN₁⊥MN₁ |
∠M₁N₁N = 90° | ⇒ ΔM₁N₁N - прямоугольный.
NM₁² = NN₁² + N₁M₁² - теорема Пифагора, следовательно:
N₁M₁ = √NM₁² - NN₁² = √(√301 см)² - 11 см² = √301 см² - 121 см² = √180 см² = √36×5 см² = 6√5 см
ответ: N₁M₁ = 6√5 см
P.S. Рисунок показан внизу↓
R=11,7см
Объяснение:
N=9 кількість сторін.
a=8см сторона дев'ятикутника
R=8/(2sin(180°/9))=8/(2*sin20°);
sin20°≈0,342
R=4/0,342≈11,7 см