Объяснение:
1.
Дано: ΔАВС.
АВ = ВС;
ВЕ - медиана;
∠АВЕ = 44°
Найти: ∠АВС; ∠FEC.
Рассмотрим ΔАВС.
АВ = ВС ⇒ ΔАВС - равнобедренный.
В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.⇒ ВЕ - высота и биссектриса.
∠АВЕ = ∠ЕВС = 44° (ВЕ - биссектриса)
⇒ ∠АВС = ∠АВЕ + ∠ЕВС = 44° + 44° = 88°
BF ⊥ АС (ВЕ - высота)
⇒ ∠FEC = 90°
2.
Дано: ΔАВС.
АВ = ВС; АО = ОС;
ОК - биссектриса.
Найти: ∠АОК.
Рассмотрим ΔАВС.
АВ = ВС ⇒ ΔАВС - равнобедренный.
АО = ОС ⇒ ВО - медиана.
В равнобедренном треугольнике медиана, проведенная к основанию, является высотой.⇒ ВО - высота, то есть ∠ВОС = 90°.
ОК - биссектриса ⇒ ∠ВОК = ∠КОС = 90° : 2 = 45°
∠АОК = ∠АОВ + ∠ВОК = 90° + 45° = 135°
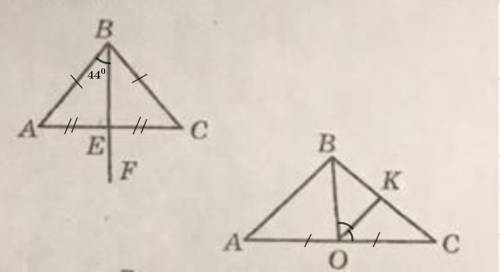
ответ: БИЛЕТ№1
1. отрезок -прямая, которая имеет начало и конец, обозначается с обоих сторон точками.
луч - это прямая линия, которая имеет начало, но не имеет конца.
угол - это геометрическая фигура, образованная 2-мя лучами
развернутый угол-это угол, стороны которого составляют прямую
2. если две стороны и угол между ними одного треугольника соответственно равны двум сторонам между ними другого треугольника, то такие треугольники равны
3. т.к. треугольник прямоугольный, а один из углов 30гр, то второй катет будет равен половине гипотенузы 12*2=24см
4.т.к треуг.АВС равноб. следовательно углы при основании равны, а т.к. угол 1 вертикальный углу ВАС, значит они равны
2 вертик угол ВС, а следовательно они равны
угол1 = углу ВАС, угол 2 - углу ВСА
следовательно углы =
Якщо бісектриса прямокутного трикутника ділить один із катетів на відрізки 12 см і 20 см, то ці відрізки відповідають відстаням від вершини прямокутного кута до точок перетину бісектриси з катетом.
Застосуємо властивості бісектриси прямокутного трикутника: відрізок, що ділить прямокутний кут навпіл, ділить і протилежну сторону на відрізки, пропорційні до інших двох сторін трикутника.
Так як один з відрізків дорівнює 12 см, а інший - 20 см, то ми маємо відповідну пропорцію: 12/20 = BC/AB, де BC - довжина одного катета, AB - довжина другого катета.
Розв'язуємо пропорцію: 12/20 = BC/AB
Перетворюємо її: AB = (20 * BC) / 12
Застосуємо теорему Піфагора для прямокутного трикутника: AB^2 + BC^2 = AC^2
Підставляємо значення AB: [(20 * BC) / 12]^2 + BC^2 = AC^2
Спрощуємо: (400 * BC^2) / 144 + BC^2 = AC^2
Об'єднуємо дробові доданки: (400 * BC^2 + 144 * BC^2) / 144 = AC^2
Складаємо чисельник: (544 * BC^2) / 144 = AC^2
Скорочуємо дріб: (17 * BC^2) / 36 = AC^2
Тепер знаходимо площу трикутника: S = (1/2) * BC * AC
Підставляємо значення: S = (1/2) * BC * √[(17 * BC^2) / 36]
Спрощуємо: S = (1/2) * √[(17 * BC^4) / 36]
Отже, площа трикутника дорівнює (1/2) * √[(17 * BC^4) / 36].
Объяснение: