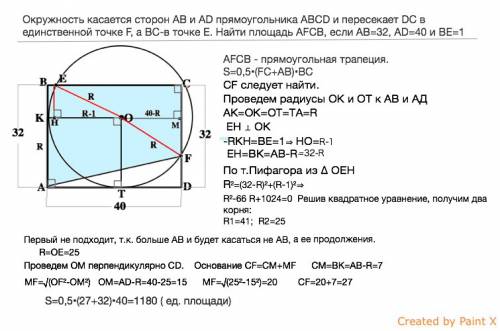
Окружность касается сторон AB и AD прямоугольника ABCD и пересекает DC в единственной точке F, а BC-в точке E.
Найти площадь AFCB, если AB=32, AD=40 и BE=1
————
АBCD- прямоугольник. ⇒
AFCB - прямоугольная трапеция. Площадь трапеции равна произведению полусуммы оснований на высоту.
S=0,5•(FC+AB)•BC
СF следует найти.
Проведем радиусы ОК и ОТ к АВ и АД соответственно.
АК=ОК=ОТ=ТА=R
Опустим из Е перпендикуляр ЕН на радиус ОК
КН=ВЕ=1⇒ НО=R-1
ЕН=ВК=АВ-R=32-R
По т.Пифагора из ∆ ОЕН
R²=(32-R)²+(R-1)²⇒
R²-66 R+1024=0 Решив квадратное уравнение, получим два корня:
R1=41; R2=25
Первый не подходит, т.к. больше, чем АВ, и будет касаться не АВ, а её продолжения.
R=ОЕ=25
Проведем ОМ перпендикулярно СD.
Основание СF=CM+MF
CM=BK=AB-R=7
MF=√(OF²-OM²)
OM=AD-R=40-25=15
MF=√(25²-15²)=20
CF=20+7=27
S=0,5•(27+32)•40=1180 ( ед. площади)
1.серединные перпендикуляры к сторонам остроугольного треугольника ABC пересекаются в точке О так, что расстояние от этой точки до стороны AC равно 8. найдите длину отрезка CO если AC= 30
2.сторона MP треугольника mkp равна 24. серединные перпендикуляры к сторонам этого треугольника пересекаются в точке D причём DP= 13. Найдите расстояние от точки D до стороны MP
3.серединные перпендикуляры к сторонам остроугольного треугольника ABC пересекаются в точке О. на стороне BC основанием серединного перпендикуляра является точка K. известно что OK= 9, KC= 12. Найдите АО
1. 32
2. 13
3. 21
4. 15
4.серединные перпендикуляры к сторонам треугольника ABC пересекаются в точке О. расстояние от точки О до стороны АС равно 6 см, а до стороны BC равно 8 см. отрезок OB имеет длину 10 см. найдите сторону AC ответ дайте в сантиметрах
1. 12 см
2. 6 см
3. 8 см
4. 16 см
5. В треугольнике ABC серединные перпендикуляры пересекаются в точке О. Известно, что угол AOC равен 120 ГРАДУСОВ, АС =30 Найдите OB. ответ дайте в сантиметрах
1.
2.
3.
4.
Відповідь:
Для початку побудуємо рисунок чотирикутної піраміди SABCD з усіма ребрами, які дорівнюють одне одному:
S
/|\
/ | \
/ | \
/ | \
ADB
| | |
| | |
| | |
CEC
У нас є чотирикутна піраміда SABCD, де всі ребра мають однакову довжину. Позначимо цю довжину як "a".
Далі побудуємо переріз піраміди площиною, яка проходить через точку D перпендикулярно до ребра SA. Оскільки ребра піраміди дорівнюють одному одному, переріз буде кругом, і цей круг буде перпендикулярним до основи піраміди.
S
/ \
/ \
/ \
/\
A C B
Знайдемо площу перерізу. Оскільки круг є колом, площа перерізу буде рівна площі кола.
Формула для обчислення площі кола: S = π * r^2
У нашому випадку, радіус кола буде рівний половині довжини ребра піраміди, тобто r = a / 2.
Тоді площа перерізу буде:
S = π * (a / 2)^2
S = π * (a^2 / 4)
Для заданого ребра піраміди a = 10 см, підставимо це значення в формулу:
S = π * (10^2 / 4)
S = π * 100 / 4
S = 25π
Отже, площа перерізу піраміди становить 25π квадратних сантиметрів.
Пояснення: