Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство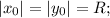
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) 
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
;
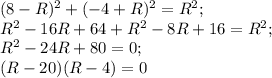R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
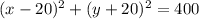
и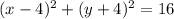 
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство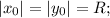 учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
;
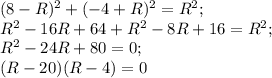R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
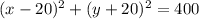
и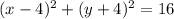
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили
Объяснение:
Для знаходження площі кільця, утвореного вписаними та описаними колами навколо трикутника, нам спочатку потрібно знайти радіуси цих колів.
Радіус вписаного кола (r) можна обчислити за формулою:
r = площа трикутника / півпериметр трикутника
Півпериметр трикутника (s) можна знайти, застосовуючи формулу:
s = (a + b + c) / 2,
де a, b, c - довжини сторін трикутника.
Площу трикутника (A) можна обчислити за формулою Герона:
A = √(s(s-a)(s-b)(s-c))
Для знаходження радіусу описаного кола (R) можна використовувати формулу:
R = abc / 4A
Отже, почнемо розрахунок:
a = 13 см, b = 15 см, c = 14 см.
Спочатку обчислимо півпериметр трикутника:
s = (13 + 15 + 14) / 2 = 21.
Потім знайдемо площу трикутника:
A = √(21(21-13)(21-15)(21-14)) ≈ 84.15 см².
Тепер можемо обчислити радіус вписаного кола:
r = 84.15 / 21 ≈ 4 см.
Нарешті, знайдемо радіус описаного кола:
R = (13 * 15 * 14) / (4 * 84.15) ≈ 6.32 см.
Площа кільця, утвореного вписаними та описаними колами, можна обчислити, віднімаючи площу вписаного кола від площі описаного кола:
S = πR² - πr²
S = π(6.32²) - π(4²)
S ≈ 125.6 - 50.24
S ≈ 75.36 см².
Отже, площа кільця навколо даного трикутника становить приблизно 75.36 см².