1) Площадь сектора прямо пропорциональна величине угла, поэтому искомый угол х меньше 360 град. во столько же раз, во сколько 15п см^2 меньше 36п см^2 (15/36), т.е. х=150
2) Пусть все рёбра по а, тогда площадь основания
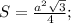 .
.
Высота тетраэдра H, высота боковой грани h и отрезок, соединяющий основания этих высот m (он равен трети медианы основания, т.к. высота тетраэдра падает в центр треугольника) связаны теоремой Пифагора:
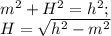
m=h/3, т.к. все треугольники равны.
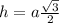 как высота правильного треугольника.
как высота правильного треугольника.
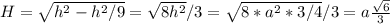 ;
;
Объём
![V=SH/3=\frac{a^2\sqrt3}{4}*a\frac{\sqrt6}{3}/3=a^3\sqrt2/12;\\ a=\sqrt[3]{12V/\sqrt2};\\](/tpl/images/0148/7418/56743.png)
Всего рёбер 6, значит
![6a=6\sqrt[3]{12V/\sqrt2}](/tpl/images/0148/7418/98a23.png)
60 см.
Объяснение:
Гіпотенуза даного трикутника 25 см (за властивістю єгипетського трикутника)
Р=15+20+25=60 см.