2.Скорее всего имелось ввиду 9 САНТИМЕТРОВ. Если 9 МЕТРОВ, то и радиус шара будет практически таким же :))) хотя можно вычислть и это. Но я буду считать, что d = 9 см. r -радиус сечения. 2*pi*r = 24*pi; r= 12; R - радиус шара, R^2 = d^2+r^2;
R = 15. высота сегмета равна h = R - d = 6, объем V = pi*6^2*(15-6/3) = 468*pi;
3. высота конуса d = 2*R/3 = 4, высота сегмента h = R - d = 2;
V = pi*2^2(6 - 2/3) = pi*64/3;
4. высота сегмента h = 2*R/6 = R/3 = 2; высота конуса d = 4 (смотри 3.)
Объем конуса pi*(R^2 - d^2)*d/3 = pi*(36 - 16)*4/3 = 80*pi/3;
складываем с ответом из 3., получаем объем сектора = 144*pi/3 = 48*pi.
Это шестая часть всего шара :)))
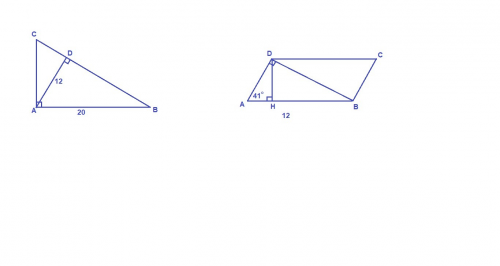
1. Из прямоугольного треугольника ABD по теореме Пифагора:
BD = √(AB² - AD²) = √(20² - 12²) = √(400 - 144) = √256 = 16 см
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота делит гипотенузу:
AD² = BD · DC
DC = AD² / BD = 144 / 16 = 9 см
ВС = BD + DC = 16 + 9 = 25 см
Из прямоугольного треугольника АВС по теореме Пифагора:
AC = √(BC² - AB²) = √(625 - 400) = √225 = 15 см
cos∠C = AC / BC = 15 / 25 = 3/5 = 0,6
2. ΔABD: ∠ADB = 90°,
cos∠A = AD / AB
AD = AB · cos 41° ≈ 12 · 0,7547 ≈ 9,1 см
ΔADH: ∠AHD = 90°,
sin∠A = DH / AD
DH = AD · sin41° ≈ 9,1 · 0,6561 ≈ 6 см
Sabcd = AB · DH ≈ 12 · 6 ≈ 72 см²