Решить данную задачу в 7 классе невозможно, поскольку она решается через теорему синусов, а это 9 класс! Возможно было бы решить задачу, если бы ∠BAD равнялся 115°, либо ∠BCF равнялся 55°. Тогда бы мы доказали, что ΔABC - равнобедренный и указали бы, что сторона AB равняется 5 см ( по свойству).
Что поделаешь: рассмотрим решение через теорему синусов.
Вертикальные углы равны.
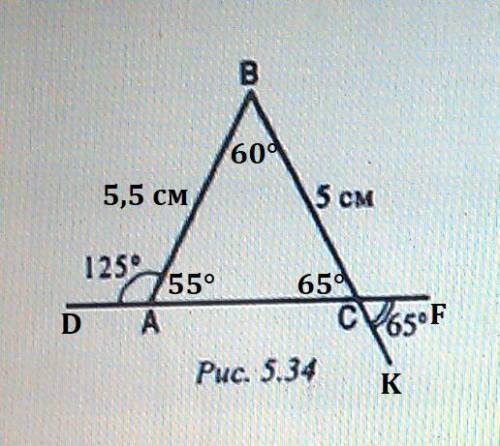
⇒ ∠FCK=∠BCA=65°, так как они вертикальные.
Сумма смежных углов равна 180°.
⇒ ∠BAD+∠BAC=180°, так как они смежные ⇒ ∠BAC=180°-125°=55°.
Сумма углов треугольника равна 180°.
⇒ ∠ABC=180°-(55°+65°)=180°-120°=60°.
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
AB:sinBCA=AC:sinABC=BC:sinBAC ⇒
AB=BC*((sinBCA)/(sinBAC)) ⇒
AB=5*((sin65°)/(sin55°))≈5*(0,906/0,819)≈5,5 (см).
ответ: AB≈5,5 (см).
(R-r)/R = l/L, где R и r - радиусы оснований, l-образующая ус. конуса, а L-образующая полного конуса.
(R-r)L = lR; L = lR/(R-r).
l = √(h²+(R-r)²) = √(24²+(14-10)²) = √592 = 4√37 см.
L = lR/(R-r) = 4√37*14/(14-10) = 14√37 см. Радиус развёртки равен образующей.
Угол развёртки:
φ = 2πR/L = 2π*14/(14√37) = 2π/√37
S = π(R+r)l + πr²= π(14+10)4√37 + 100π = π(96√37+100) ≈ 2 148.67 см² ≈ 21.5 дм²