задача 1
1) исходя из условия, что относятся как 6/6/7 (как длина/ширина/высота), то AB=BC=CD=AD=6, ABCD - квадрат.
2) диагональ нижней и верхней грани, а миенно квадрата, равна "а" корень из 2, где "а" - сторона квадрата. Следовательно AC=6 корней из 2
3) С1С=7
BC=6
из т. Пифагора найдем C1D= корень из85
ответ: AB1=B1C=C1D=A1D=корень из 85
B1D=BD=6корней из 2
задача 2
Скрещивающиеся прямые. Если две прямые не лежат в одной плоскости не параллельны одна другой и не пересекаются, они называются скрещивающимися.
наименьшее ребро 2, а именно СС1=DD1=AA1=BB1=2
скрещивающиеся прямые тут - AD и CD , например, а расстояние и естьAD = 4
задача3
середіна AA1 - L, если не ошибаюсь сечение есть треугольник B1CD

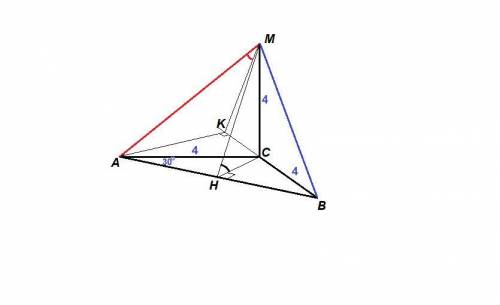
a) tg∠MHC = 2
б) ∠(AM; (MBC)) = arccos(√10/4)
Объяснение:
a) Пусть Н - середина АВ, тогда СН - медиана и высота равнобедренного треугольника АВС,
СН ⊥ АВ.
СН - проекция МН на плоскость (АВС), значит
МН ⊥ АВ по теореме о трех перпендикулярах.
Тогда ∠МНС - линейный угол двугранного угла МАВС.
Из прямоугольного треугольника АСН:
СН = АС/2 = 2 см, как катет, лежащий против угла в 30°.
ΔМНС: ∠МСН = 90°,
tg∠MHC = MC / CH = 4 / 2 = 2
б) ∠ВАС = ∠ВСА = 30° как углы при основании равнобедренного треугольника АВС, ⇒
∠АСВ = 180° - 30° · 2 = 120°
Проведем АК⊥ВС, тогда ∠ АСК = 180° - 120° = 60° (по свойству смежных углов).
ΔАСК: ∠АКС = 90°
∠САК = 90° - 60° = 30°.
КС = 1/2 АС = 2 см как катет, лежащий против угла в 30°.
ΔСКМ: ∠МСК = 90°, по теореме Пифагора
МК = √(МС² + СК²) = √(16 + 4) = √20 = 2√5 см
СМ⊥(АВС) по условию, значит
СМ⊥АК,
АК⊥ВС по построению, ⇒ АК ⊥ (МВС), тогда
МК - проекция прямой АМ на плоскость (МВС) и значит
∠АМК = ∠(АМ; (МВС)) - искомый.
ΔАМС прямоугольный равнобедренный, значит его гипотенуза
АМ = СМ√2 = 4√2 см
ΔАМК: ∠АКМ = 90°
cos∠AMK = MK / AM = 2√5 / (4√2) = √10/4
∠AMK = arccos(√10/4)