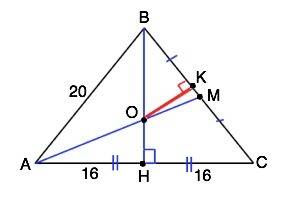
Обозначим медианы ВН и АМ.
В равнобедренном треугольнике медиана, проведенная к основанию, является высотой и биссектрисой. =>
∆ АВН - прямоугольный, АН=СН=32:2=16 см
По т.Пифагора
ВН=√(AB²-AH²)=√(400-256)=12
Медианы треугольника точкой пересечения делятся в отношении 2 :1, считая от вершины.=>
ВО=ВН•2/3=8
ОН=ВН:3=4
Из прямоугольного ∆ АОН по т.Пифагора
АО=√(AH*+OH*)=√(256+16)=√272=4√17
Расстояние от точки до прямой измеряется длиной отрезка, проведенного от точки перпендикулярно к прямой.
ОК⊥ВС
Прямоугольные ∆ ОКВ и ∆ ВНС имеют общий острый угол при В. => они подобны.
ОВ:ВС=ОК:НС
8:20=ОК:16 =>
20•ОК=128
ОК=6,4 (см)
1) с²=5²+6²
с=√61
2) с²=1²+1²
с=√2
3) с²=1,5²+2²
с=√6,25
с=2,5
4) с²=0,8²+0,6²
с=√0,64+0,36
с=√0,1