8 см
Объяснение:
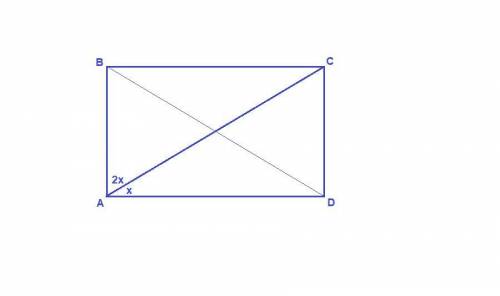
Диагональ АС делит угол А, равный 90°, в отношении 1 : 2.
Пусть ∠DAC = x, тогда ∠BAC = 2x.
x + 2x = 90°
3x = 90°
x = 30°
∠BCA = ∠DAC = 30° как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АС.
ΔАВС: ∠АВС = 90°, против угла в 30° лежит катет, равный половине гипотенузы, т.е. АС = 2АВ.
По условию АС + BD + AB + CD = 24,
диагонали прямоугольника равны, противоположные стороны равны, поэтому
2АС + 2АВ = 24
АС + АВ = 12
так как АС = 2АВ, получаем:
2АВ + АВ = 12
3АВ = 12
АВ = 4 см,
АС = 2АВ = 2 · 4 = 8 см
Квадрат высоты = 16, квадрат диагонали = 41.
Объяснение:
Равнобедренную трапецию можно представить как три отдельные фигуры: два прямоугольных треугольника, равных между собой, и прямоугольник.
Из условия задачи мы знаем гипотенузу прямоугольного треугольника - это 5. Мы можем найти один из его катетов - это будет половина разности двух оснований трапеции: (8 - 2)/2 = 3. Соответственно, второй катет будет высотой трапеции, и мы находим его по теореме Пифагора: 5^2 = 3^2 + x^2. х = sqrt(25-9) = 4 (треугольник с таким соотношением сторон называется египетским). Соответственно, квадрат высоты трапеции будет 4^2 = 16.
Диагональ равнобедренной трапеции можно найти по формуле: квадратный корень из суммы квадрата боковой стороны и произведения обоих оснований. d = sqrt (c^2 + ab) = sqrt(5^2 + 2*8) = sqrt(25+16) = sqrt(41). Для решения задачи не нужно находить саму диагональ, достаточно ее квадрата: sqrt(41)^2 = 41.