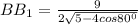
Объяснение:
оловине гипотенузы ВС (СН=1/2CD, СD=BC как стороны ромба). Используем свойство прямоугольного треугольника: если катет прямоугольного треуг-ка равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°. Значит
<CBH=30°
Зная, что сумма острых углов прямоугольного треугольника равна 90°, находим угол С:
<C=90-<CBH=90-30=60°, что и требовалось доказать.
2. ВМ=АВ-AM, CL=BC-BL, DP=CD-CP, AQ=AD-DQ, но
АМ=BL=СР=DQ по условию, а АВ=BC=CD=AD как стороны квадрата. Значит
ВМ=CL=DP=AQ
Прямоугольные треугольники MAQ, LBM, PCL и QDP равны, таким образом, по двум сторонам и углу между ними (углы А, B, C, D - прямые, АМ=BL=СР=DQ по условию, ВМ=CL=DP=AQ как только что доказано). У равных треугольников равны и соответственные стороны MQ, LM, LP и PQ. Значит, MLPQ-квадрат.
Высота, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу: . Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, делит его на два подобных и подобных исходному треугольнику.
Высота, проведённая из вершины прямого угла на гипотенузу, есть средняя пропорциональная между отрезками гипотенузы, а каждый катет есть среднее пропорциональное между всей гипотенузой и своей проекцией на гипотенузу. Доказательство. Вот наш прямоугольный треугольник ABC, вот его гипотенуза AB, вот высота CH, проведённая из вершины прямого угла на гипотенузу. И вот отрезки, на которые высота делит гипотенузу: AH и BH. И нам надо доказать, что высота — это среднее пропорциональное между отрезками гипотенузы, то есть AH/CH = CH/BH, доказать, что каждый катет — это среднее пропорциональное между гипотенузой и своей проекцией на гипотенузу, то есть AB/AC=AC/AH и AB/BC=BC/BH. Все эти три равенства следуют из подобия трёх изображённых треугольников ▲ACH, ▲BCH и исходного треугольника ▲ABC. Докажем сначала подобие ▲ACH и ▲ABC. У обоих этих треугольников равные прямые углы, и равные углы с кружком — то есть треугольники подобны по первому признаку, и третьи углы (с зубчиками) у них тоже равны. У треугольников ▲BCH и ▲ABC тоже равные прямые углы и равные углы с зубчиками — выходит, эти треугольники тоже подобны по первому признаку, и третьи углы (с кружком) у них тоже равны. У треугольников ▲ACH и ▲BCH тоже равные прямые углы и углы с кружком, и эти треугольники тоже подобны по первому признаку.
Подобие трёх треугольников доказано.
В подобных треугольниках ACH и BCH отношения короткого и длинного катетов равны — а это как раз наше первое равенство. В подобных треугольниках ACH и ABC отношения гипотенузы и короткого катета равны — это наше второе равенство.
В подобных треугольниках BCH и ABC отношения гипотенузы и длинного катета равны — и это наше третье равенство.
Равенства доказаны — а их и надо было доказать.