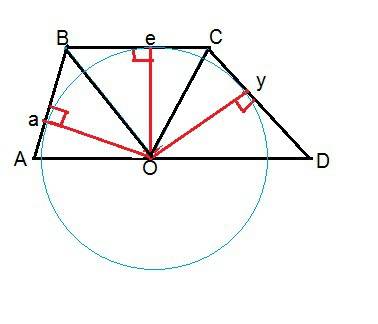
Проведем из О к указанным сторонам трапеции перпендикуляры к АВ -а, к ВС - е, к СD-у
Рассмотрим ∆ ВОа и ВОе. Они прямоугольные , имеют общую гипотенузу ВО и по равному острому углу при В.
Если гипотенуза и прилежащий к ней угол одного прямоугольного треугольника соответственно равны гипотенузе и прилежащему углу другого треугольника, то такие треугольники равны. ⇒
катет аО = еО
Аналогично доказывается равенство катетов еО и уО треугольников СОе и СОу.
Отрезки Оа, Ое, Оу равны и как перпендикуляры от точки до прямой, являются расстоянием от О до АВ, до ВС и до AD.
Т.е. О - равноудалена от прямых АВ, ВС и AD, ч.т.д.
Как вариант: Из теоремы:
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон, следует:
Точка О - общая для биссектрис двух углов с общей стороной ВС, следовательно, равноудалена от прямых, содержащих их стороны.
Тело вращения представляет из себя цилиндр с высотой, равной меньшей стороне треугольника 13 см и радиусом оснований 16 см, из которого "вырезаны" усеченные конусы с равными радиусами и образующими 14 см и 15 см.
–––––––––––––––––––––––––––––––––––––––
Искомая площадь - сумма боковых поверхностей этих усеченных конусов S1+S2 и боковой поверхности цилиндра S3.
а) Для решения нужно найти радиус меньшей окружности, которая образуется при вращении вершины треугольника, противолежащей меньшей стороне.
Найдем высоту треугольника, проведенную к меньшей стороне, из его площади. Площадь треугольника со сторонами 13,14,15 встречается часто и равна 84 ( проверьте по ф.Герона)
Высота равна 168:13=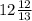 см
см
Радиус меньшей окружности равен R-h
Формула боковой поверхности усеченного конуса
Ѕ=πRL•(R+r)⇒
S1=π•14•(16+3,0769)=267,0766π см²
S2=π•15•(16+3,0769)=286,1535π см²
По формуле боковой поверхности цилиндра
S3=2πr•13=32•π•13=416π см²
S=969,2301π см² или ≈ 3044,926 см²