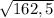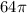см³.
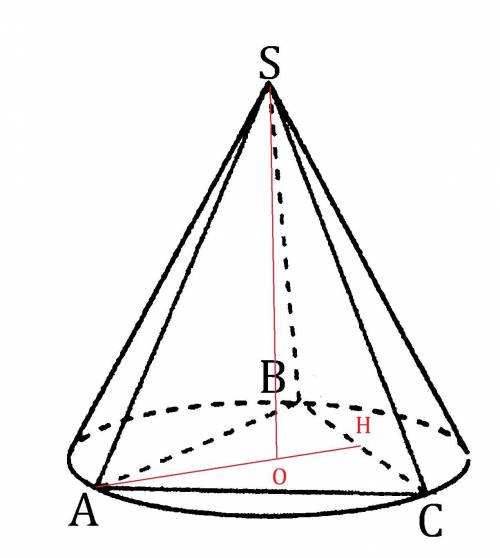
Обозначим данную пирамиду буквами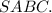 
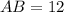см.
Проведём высоту пирамиды SO.
Начертим около этой пирамиды конус.
Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.
=======================================================
Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.
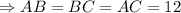см.
Проведём высоту 
в 
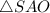- прямоугольный, так как 
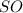- высота пирамиды.
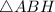- прямоугольный, так как - высота .
Так как - равносторонний ⇒ - высота, медиана и биссектриса
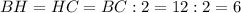см, так как - медиана.
Найдём по теореме Пифагора 
.
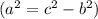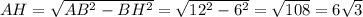см.
Точка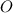 
- пересечение медиан и делит их в отношении 
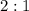, считая от вершины.
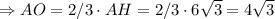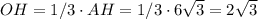см
см.
Также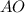 
- радиус описанной около окружности.
Рассмотрим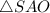
Если угол в прямоугольном треугольнике равен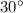 
, то напротив лежащий катет равен половине гипотенузы.
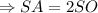
Составим уравнение:
Пусть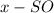 
, тогда 
.
И по теореме Пифагора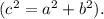 
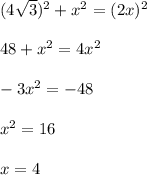
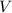конуса = 
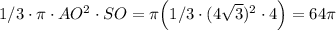см³.
Дано: А(-3; 9), В(-4; -8), С(6; 0)
Найти:
а)координаты вектора АС;
б)длину вектора ВС;
в)координаты середины отрезка АВ:
г)периметр треугольника АВС;
д)длину медианы СМ.
a) AC = {Cx - Ax ; Cy - Ay}
AC = {6 - (-3) ; 0 - 9}
AC ={9 ; -9}
б) BC = {Cx - Bx ; Cy - By}
BC = {6 - (-4); 0 - (-8)}
BC = {10 ; 8}
|BC| = 
= 
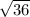= 6
в) Пусть это будет точка M, тогда её координаты будут равны
M((Ax + Bx)/2 ; (Ay + By)/2)
M((-3 + -4)/2 ; (9 + 8)/2)
M(-3,5 ; 8,5)
г) Посчитаем длину каждой стороны треугольника
AB =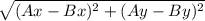 
= 
= 
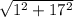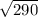
AC =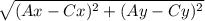 
= 
= 
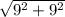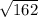
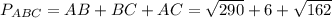
д) СМ =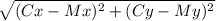 
= 
= 
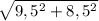