а) Координаты середины отрезка равны полусуммам соответствующих координат его концов.
А (2; -1; 0), В (-4; 2; 2)
Обозначим середину отрезка АВ буковой К
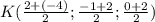
К (-1; 0,5; 1)
б) Нужно найти координаты точки С, если точка В является серединой отрезка АС. Координаты точек А и В известны. Координаты точки С обозначим (x; y; z). И используем формулу для нахождения координат середины отрезка. Находим координаты середины отрезка АС.
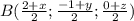
Координаты точки В известны. Приравняем их и получим три уравнения, решая которые найдем координаты точки С.
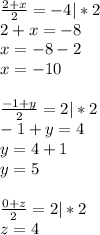
C (-10; 5; 4)
в) Длина отрезка можно вычислить так: квадратный корень из суммы квадратов разностей соответствующих координат концов отрезка.
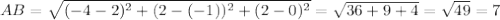
АВ=7
1)В; 2)Б; 3)Г; 4)В: 5)Б
Объяснение:
1. число должно делится на 4, т.к у ромба все стороны равны.
2. два угла по 65°=130°, (360-130)/2=115°
3.формула периметра параллелограмма по Р=2(х+у), отсюда у=(Р-2х)/2
4. диагонали параллелограмма при пересечении образуют со сторонами равнобедренные треугольники. У равнобедренных треугольников углы при основании равны. Имеем два угла по 20° , значит оставшийся угол равен (180-20-20)=140; (180- это сумма всех углов любого треугольника)
5. Если диагональ перпендикулярна стороне, значит она образует с этой стороной угол 90°. Второй угол дан по условию -20°, Третий угол =(180-90-20) =70°
а)
ABCD - прямоугольник. МВ перпендикулярна плоскости АВСD.
МА - наклонная, АВ - ее проекция. АВ⊥АD.
По т.о 3-х перпендикулярах МА⊥AD ⇒ ∆ МАD- прямоугольный.
МС - наклонная, – ВС её проекция.
По т.о 3-х перпендикулярах МС⊥СD – ∆ МСD- прямоугольный. ч.т.д.
б)
АВ=МВ:tg45°=4:1=4 (см)
ВС=MB:tg30°=4:(1/√3)=4√3
CD=AB=4; AD=BC=4√3
в)
MD - наклонная, BD - её проекция.
ВС - проекция наклонной МС.⇒
∆ BDС - проекция ∆ MDС на плоскость АВСD.
S∆ BCD=BC•CD:2=4√3•4:2=8√3 см²