Из площади трапеции ABCD найдем высоту трапеции CH
\displaystyle \tt S_{ABCD}=\frac{AD+BC}{2}\cdot CH~~~\Rightarrow~~~ CH=\frac{2S_{ABCD}}{AD+BC} =\frac{2\cdot84}{4+3}= 24S
ABCD
=
2
AD+BC
⋅CH ⇒ CH=
AD+BC
2S
ABCD
=
4+3
2⋅84
=24
Так как AD || MN и BC || MN, то CK ⊥ MN. Высота CK в два раза меньше высоты CH, т.е. CK = 24/2 = 12.
Средняя линия трапеции равна полусумме основания,т.е.
\tt MN=\dfrac{AD+BC}{2}=\dfrac{4+3}{2}=3.5MN=
2
AD+BC
=
2
4+3
=3.5
\tt S_{BCNM}=\dfrac{MN+BC}{2}\cdot CK =\dfrac{3.5+3}{2}\cdot12= 57S
BCNM
=
2
MN+BC
⋅CK=
2
3.5+3
⋅12=57 кв. ед.
ответ: 57 кв. ед..

70
Объяснение:
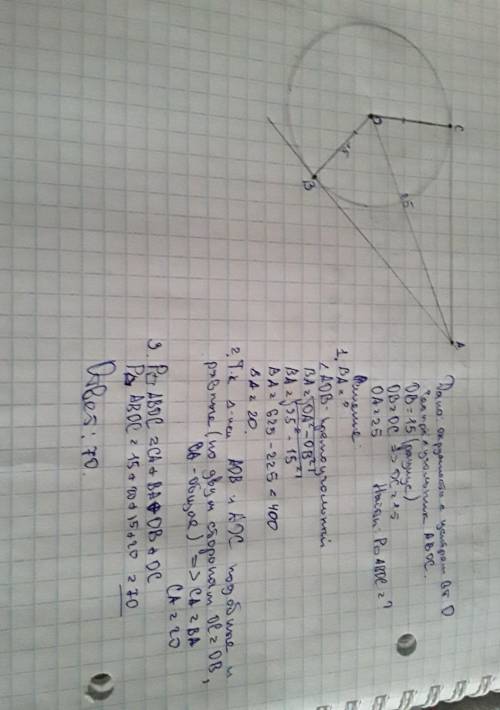
скорее всего ты ошибся(-лась) и там четырех угольник АВОС.
И так, сначала чертим окружность с центром в точке О. проводим к нет две касательные из точки А (т.к. касательные выходят из одной точки). проводим два радиуса ОВ и ОС, и биссектрису угла О (скажем так, в условии про биссектрису не пишем) ОА. Получим четырехугольник АОВС. так как прямая ОА делит его на два равных треугольника, нам нужно найти одну сторону (либо СА, либо ВА). я искала через треугольник АОВ. нам известен катет и гепотенуза, второй катет ищем через теорему Пифагора ( квадрат гипотенузы равен сумме квадратов катетов). в нашем случае: чтобы найти неизвестный катет нужно от квадрата гнпотенузы отнять квадрат известного катета. далее находим периметр. периметр это сумма длин сторон. значит нам нужно сложить ОС, ОВ, ВА и АС. после сложения получаем 70.
P.S: если здесь я объяснила не понятно, то я прикрепила фото с решением (сорри за почерк)
AD=A1D1=B1C1=5 противолежащие стороны прям. параллелепипеда
ответ. 5см