Так как вписан прямоугольный треугольник CKB угол CKB — прямой, а следовательно и угол AKB тоже прямой, так как они смежные.
CB=45 и AB=60 — катеты, AC — гипотенуза
По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы.
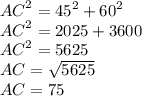
CK+KA=75
KA=CK+21
CK+(CK+21)=75
2CK=75-21
2CK=54
CK=27
KA=27+21=48
Найдем длину BK по той же теореме Пифагора:
CB²=CK²+BK²
BK²=CB²-CK²
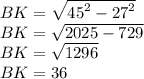
Найдем площадь треугольника AKB по формуле S=(ab)/2, где a и b катеты
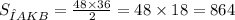
Теперь найдем площадь треугольника CKB:
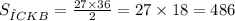
Отношение площадей треугольников AKB и CKB
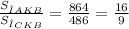
S(ΔAKB):S(ΔCKB) = 16:9
- всё это конечно углы.
ответ: 1=36, 2=144