ответ: 16 (ед. объёма)
Подробное объяснение:
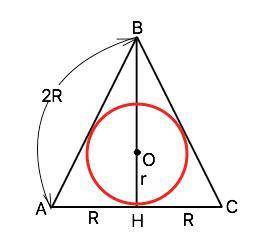
Схематический рисунок осевого сечения шара, вписанного в конус – окружность с радиусом r (радиус шара), вписанная в треугольник АВС. В данной задаче треугольник АВС правильный, его сторона равна диаметру основания конуса. ⇒ АВ=ВС=АС=d=2R
Высота ВН треугольника АВС – высота конуса ВН=АВ•sin60°=2R•√3/2=R√3. Подставим значение высоты в формулу объёма конуса:
V(к)=πR²•h/3= πR²•R√3/3=πR³/√3 ⇒ πR³/√3=36
Радиус r окружности, вписанной в правильный треугольник, равен 1/3 высоты этого треугольника ( высоты конуса). r=OH=(R√3):3=R/√3
Подставим найденное значение радиуса шара в формулу его объёма:
V(ш)=4π(R/√3)³/3=4πR³/9√3
Из найденного объёма конуса πR³/√3=36
подставим это значение в выражение объёма шара:
V(ш)=4•36/9=16 (ед. объёма)
пусть даны точки А и В. Возьмем третьею точку С отличную от А и В.
Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
проведем плоскость АВС
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Возьмем точку D не принадлежщаю плоскости АВС (таковая существует за аксиомой выше)
проведем плоскость АВD.
Єти плоскости разные так как точка D не принадлежит плоскости АВС.
и данные точки А и В принадлежат одновременно и плоскости АВС и ABD.
Таким образом существование искомых плоскостей доказано
тю, 90 градусов, как по теории. а вот решать как, не знаю.