В равнобедренном треугольнике АВС длина основания АВ равна √2, угол при основание равен 30 градусам найдите периметр треугольника.
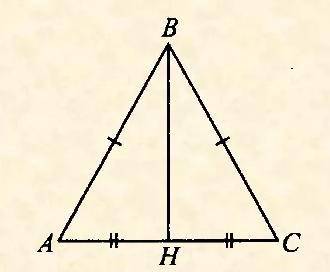
Проведем высоту АН. В равнобедренном треугольнике высота, проведенная к основанию, является также биссектрисой и медианой.
АН = АС = √2/2 (ед.)
Угол ВАС = 30° (по условию)
Тангенс есть отношение противолежащего катета к прилежащему.
tg(30)° = BH : АН
tg(30)° = BH : √2/2
√3/3 = BH : √2/2
√3/3 = √2 × BH
BH = √3/(3√2)
BH = √6/6 (ед.)
По т. Пифагора:
c² = a² + b²
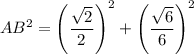
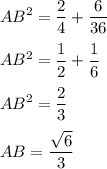
AB = √6/3 (ед.)
Так как треугольник равнобедренный:
AB = BC = √6/3 (ед.)
Периметр равнобедренного треугольника ищем по формуле:
P = 2a + b, где a - боковая сторона, b - основание.

ответ: (2√6)/3 + √2 (ед.)
гипотенуза АВ = 13,5 (по условию)
первый катет ВС = 1 м (по условию)
тогда <A - угол наклона горы
sinA = BC/AB 1/13,5 ⇒ <A = arcsin 1/13,5, приближенное значения угла можно найти в таблице синусов