1)Из центра O окружности, вписанной в трапецию, восстановлен перпендикуляр OM к плоскости трапеции.
Найдите радиус окружности, если расстояния от точки M до одной из сторон трапеции и до ее плоскости равны 3 см и 3,4 см.
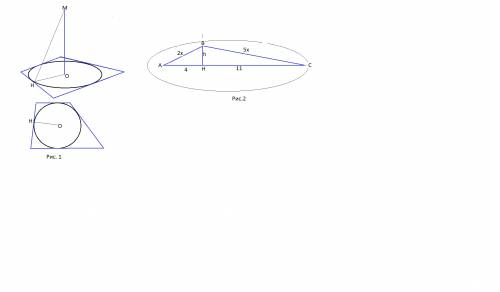
Сделаем рис.№1. Обозначим расстояние от М до стороны трапеции МН.
Расстояние между точкой и плоскостью измеряется длиной отрезка, перпендикулярного плоскости.
Следовательно, ОМ=3 cм, а расстояние МН от М до стороны трапеции=3,4 cм, так как перпендикуляр всегда короче наклонной, а МН - наклонная, проведенная перпендикулярно стороне трапеции. Любой стороне.
Ее проекция ОН также будет перпендикулярной этой стороне ( теорема о трех перпендикулярах).
Причем это относится к любой стороне трапеции - перпендикуляр из О к стороне трапеции пересекает ее в точке касания окружности и стороны, являющейся в данном случае касательной к окружности.
Этот перпендикуляр - проекция расстояния от М до стороны - и будет радиусом вписанной окружности. Найдем его по т. Пифагора:
ОН= √(МН²-ОМ²)=1,6 см
ответ: Радиус окружности равен 1,6 см
2) Из одной точки к плоскости проведены перпендикуляр и две наклонные, проекции которых равны 4 и 11 см.
Найдите длину перпендикуляра, если наклонные относятся как 2:5
Сделаем рисунок №2,
обозначим вершины получившейся фигуры привычными А, В, С.
Рассмотрим треугольник АВС, который образован наклонными АВ и ВС и их проекциями АН и НС.
Высота ВН- искомый перпендикуляр- может быть найдена из треугольников АВН и ВСН.
Выразим ее значение из этих треугольников по т.Пифагора.
ВН²=АВ²-АН²
ВН²=ВС²-НС²
Приравняем эти значения:
АВ²-АН²=ВС²-НС²
Пусть коэффициент отношения наклонных равен х. Тогда
4х²-16=25х²-121
21х²=105
х²=5
х=√5
ВН²=АВ²-АН²
ВН²=20-16=4
ВН= √4=2 см
ответ: Длина перпендикуляра - 2 см
Пусть х сантиметров - высота прямоугольника, тогда его основание равно (х + 10) см площадь этого прямоугольника равна х(х + 10) см². По условию задачи х(х + 10) = 24.
Раскрывая скобки и перенося число 24 с противоположным знаком в левую часть уравнения, получаем:
х² + 10х - 24 = 0
Разложить левую часть уравнения на множители группировки:
х² + 10х - 24
х² + 12х - 2х - 24
х(х + 12) - 2(х+12)
(х + 12)(х - 2)
Следовательно, уравнение можно записать так:
(х + 12)(х - 2) = 0
Получили: х¹ = -12; х² = 2
Дина отрезка не может быть отрицательным числом
ответ: Искомая высота прямоугольника 2 см
Множество всех точек плоскости, находящихся на данном расстоянии от данной прямой представляет собой две параллельные прямые, находящиеся на данном расстоянии от данной прямой, т.е. по обе стороныы от нее (см. рис.)