ответ: Дана правильная треугольная пирамида sabc. боковое ребро пирамиды 5 см, высота so равна 4 см. найти площадь полной поверхности пирамиды.
Боковое ребро и высота образуют прямоугольный треугольник -> находишь расстояние АО = BO = CO по теореме Пифагора
Эти расстояния еще и радиусы описанной окружности правильного треугольника => из формулы R = aV3\3 находишь a = AB = BC = AC --> стороны треугольника АВС в основании
Зная стороны, находишь S (ABC) = a^2*V3\4 - площадь АВС
Зная стороны треугольника АВС, находишь r = aV3 \ 6 - радиус вписанной окружности.
Если, например, точка К принадлежит АВ и ОК = r, то рассматриваешь прямоугольный треугольник SOK и находишь SK - высоту треугольника ASB (боковая стороны)
Зная эту высоту и основание АВ, находишь площадь S бок. стороны ASB
S полн = S (ABC) + 3*S бок
Объяснение:
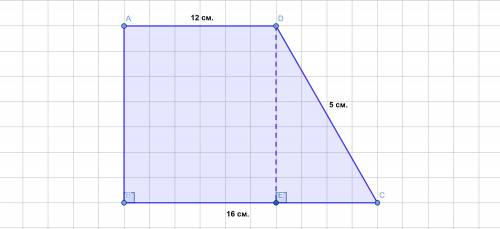
Прямоугольная трапеция.
Основания (трапеции) = 12 см и 16 см.
Боковая сторона = 5 см.
Найти:S (трапеции) = ? см².
Решение:Обозначим прямоугольную трапецию буквами ABCD.
AD - меньшее основание, BC - большее основание.
Так как любая наклонная > перпендикуляра ⇒
DC - большая боковая сторона, AB - меньшая боковая сторона, а также высота данной прямоугольной трапеции.
Проведём из точки D к большему основанию BC прямоугольной трапеции ABCD перпендикуляр DE. Этот перпендикуляр - высота.
CE = BC - AD = 16 - 12 = 4 см.
Найдём высоту DE по теореме Пифагора (a = √(b² - c²), где a и b - катеты, c - гипотенуза):
DE = √(DC² - CE²) = √(5² - 4²) = √(25 - 16) = √9 = 3 см.
⇒ S трапеции ABCD = (AD + BC)/2 * DE = (12 + 16)/2 * 3 = 42 см².
ответ: S трапеции ABCD = 42 см².