Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.
SΔ= ½ ab · sin γ
S = ½ · ¼a² · (√3)/2 =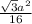 
(кв.ед.)
Из формулы площади шестиугольника S=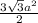
выражаем сторону а:
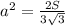
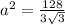
Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.
6SΔ = 16 кв.ед.
Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)
https://tex.z-dn.net/?f=S_%7BABD%7D%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20AD%5Ccdot%20BD%5Ccdot%20%5Csin%7B%5Calpha%7D%5C%5C%5C%5CS_%7BCBD%7D%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20CD%5Ccdot%20BD%5Ccdot%20%5Csin%7B(180%5E%7B%5Ccirc%7D-%5Calpha)%7D%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20CD%5Ccdot%20BD%5Ccdot%20%5Csin%7B%5Calpha%7D%5C%5C%5C%5C%5Cfrac%7BS_%7BCBD%7D%7D%7BS_%7BABD%7D%7D%3D%5Cfrac%7B1%2F2%5Ccdot%20%5Ccdot%20CD%5Ccdot%20BD%5Ccdot%20%5Csin%7B%5Calpha%7D%7D%7B1%2F2%5Ccdot%20AD%5Ccdot%20BD%5Ccdot%20%5Csin%7B%5Calpha%7D%7D%3D%5Cfrac%7BCD%7D%7BAD%7D%3D%5Cfrac%7B13x%7D%7B2x%7D%5C%5C%5C%5CS_%7BCBD%7D%2BS_%7BABD%7D%3D75%3D15x%5CRightarrow%20x%3D5%5C%5C%5C%5CS_%7BABD%7D%3D2x%3D10%5C%5C%5C%5COtvet%5C!%5C!%3A%5C%3B10.
Объяснение:
Первая часть задачи решена Пользователем 5SashaRyskin5.
Добавлен рисунок и нахождение двух других высот.
P=64, cos A=cos C=0,28. BD-высота. Найди: BD.
1) Cos A=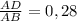
AC+2AB=64, AC=2AD, 2AD+2AB=64, 2*(AD+AB)=64, AD+AB=32.
AB=32 - AD.
Пусть х=AD, тогда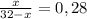
Решаем уравнение.
224 - 7x = 25x
х=7. AD=7, АB=32-7=25.
Рассмотри треугольник ABD.
BD=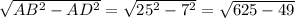
= 24
ответ: BD=24 см.
2) AC = 2AD = 7 · 2 = 14 см
Sabc = 1/2 · AC · BD = 1/2 · AB · CH
CH = AC · BD / AB = 14 · 24 / 25 = 13,44 см
АК = СН = 13,44 см как высоты, проведенные к равным сторонам.