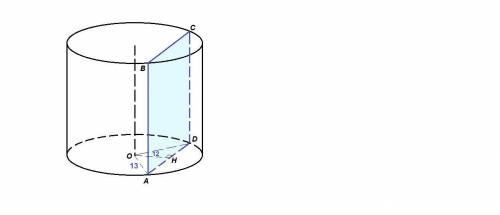
Радиус основания цилиндра равен 13 см, площадь сечения цилиндра плоскостью, параллельной оси цилиндра, равна 80 см², расстояние от плоскости сечения до оси цилиндра равно 12 см. Найдите высоту цилиндра
.
ответ: 8 см
Объяснение:
OA = OD = R = 13 см
Проведем ОН⊥AD. ОН лежит в плоскости основания, АВ - перпендикуляр к плоскости основания, значит ОН⊥АВ.
Тогда ОН⊥(АВС),
ОН = 12 см - расстояние от оси цилиндра до плоскости сечения.
ΔАОН: ∠АНО = 90°, по теореме Пифагора
АН = √(АО² - ОН²) = √(13² - 12²) = √(169 - 144) = √25 = 5 см
ОН - высота равнобедренного треугольника AOD, значит ОН и медиана, ⇒
AD = 2АН = 10 см
ABCD - прямоугольник,
Sabcd = AD · АB = 80
АB = Sabcd : AD = 80 : 10 = 8 см
2)В правильном четырехугольнике периметр равен 4a (за a взята сторона)
3)Через формулу:an =2R * sin 180/n (где R- радиус описанной окружности, а n обозначает количество сторон правильного многоугольника, в данном случае формула выглядит так:
a4 =2R * sin 180/4 (заметьте, что в данной формуле a4 обозначает сторону четырехугольника, а не просто a умноженное на 4)
4)a4 =2R * sin 180/4=2R * sin 45 = 2R * (корень из 2/ на 2)= R * (корень из 2)
А так как нам нужна не одна сторона, а весть периметр, то мы полученное выражение умножаем на 4 (так стороны 4):
P=4* R * ( корень из 2)
5) из формулы r=R * cos 180/n выразим радиус вписанной окружности r для нашего четырехугольника:
r= R* cos 180/4= R * cos 45= R * (корень из 2/2)
5)Подставим все полученные значения в формулу из пункта 1
32=1\2 *R *(корень из 2) * 4 *R *(корень из 2/ на 2)
32=2R^2
R^2=16
R=4
6) В формулу длинны окружности подставляем полученное значение:
C=2*4* (число пи)
C=8* 3,1416= 25,13274...
ответ: 25,13274