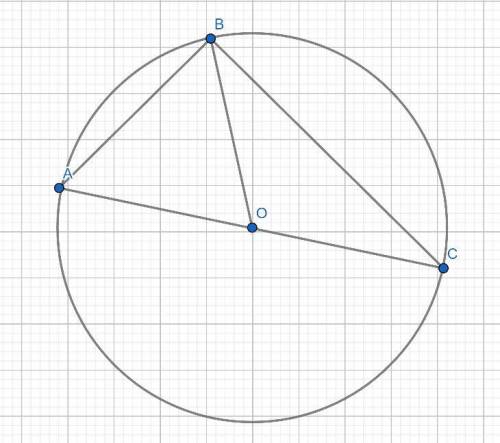
Дан прямоугольный ΔABC с прямым углом B. BO - медиана, проведенная из вершины прямого угла. Опишем около ΔABC окружность. Тогда гипотенуза AC будет являться диаметром окружности, так как вписанный угол ABC является прямым, то он опирается на диаметр окружности.
Медиана в треугольнике является отрезком, опущенным из вершины треугольника на середину противолежащей стороны. BO делит AC пополам. BO соединяет точку на окружности и центр окружности - тч.О, т.е. является радиусом окружности.
Отрезки BO = AO = OC - являются радиусами одной и той же окружности. ⇒ BO = AC/2.
На стороне BC остроугольного треугольника ABC (AB ≠ AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 32, MD = 8, H — точка пересечения высот треугольника ABC. Найдите AH.
Решение.
Проведём построения и введём обозначения как указано на рисунке. Угол — вписанный, опирающийся на диаметр, поэтому он равен 90°. Значит, точка пересечения прямых и — точка пересечения высот Продолжим высоту до пересечения с окружностью в точке Получаем, что По теореме о секущих получаем, что Треугольники и — прямоугольные, угол — общий, следовательно, эти треугольники подобны, откуда:
ответ: 30.