
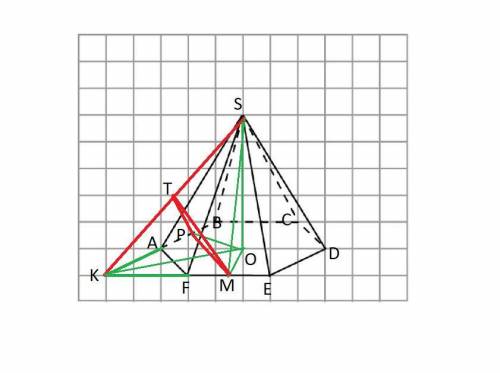
Отрезок KS - линия пересечения заданных плоскостей.
Проекция апофемы на основание равна радиусу вписанной окружности.
r = OM = 2*cos30° = 2*(√3/2) = √3.
Высота пирамиды Н = √(17 - 2²) = √13.
Отрезок КО равен 2√3.
Длина KS = √(13 + (2√3)²) = √25 = 5.
Из точек М и Р проводим перпендикуляры к KS.
Длина МР как средняя линия трапеции ABEF равна (2 + 4)/2 = 3.
Апофема SM равна √(13 + (√3)²) = √16 = 4.
Отрезки РТ и МТ = 3*sin(MKS) = 3*(4/5) = 12/5.
Искомый угол равен:
α = 2arc sin((3/2)/(12/5) = 2arc sin(5/8) = 77,36437°.
Объяснение:
3 задача
так как 1 угол равен 90 градусов, то это прямоугольный треугольник.
в прямоугольном треугольнике катет лежащий против угла 30 градусов равен половине гипотенузы.
PD=1,2см и лежит напротив угла Q(30 градусов) значит PD равен половине гипотенузы(наибольшая сторона треугольника - PQ), значит PQ = 2PD
PQ = 1,2 * 2 = 2,4
4 задача
так как 1 угол равен 90 градусов, то это прямоугольный треугольник.
обратное свойство прямоугольного треугольника: если катет(сторона) равен половине гипотенузы(наибольшая сторона треугольника), то он(катет) лежит против угла 30 градусов.
AB = 4,2см это половина гипотенузы(CB), значит AB лежит против угла 30 градусов, то есть угол C равен 30 градусов.
Нужно найти угол B.
можно использовать два
первый
сумма всех углов треугольника равна 180 градусов. Чтобы найти угол B нужно вычесть из 180 градусов угол A(90 градусов) и угол C(30 градусов) получаем, что угол B = 60 градусов
второй
в прямоугольном треугольнике один угол равен 90 градусов, и сумма двух других равна 90 градусов.
значит нужно из 90 градусов вычесть угол C(30 градусов) значит угол B равен 60 градусов