Объяснение:
3. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-7°=83° .
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=83°.
4. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-84°=6°
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=6°.
5. ∠ ABC =90°(вписанный), т.к ∪ АС=180° (опирается на диаметр АС). Тогда ∠С=180°-90°-75°=25°
6. 1) ∪ AN=73°·2=146° (стягивает вписанный ∠ NBA). Тогда
∪ NB =∪ AB-∪AN=180°-146°=34°.
2) ∠NMB=34°/2=17° (вписанный не центральный угол)
7. 1) ∆ АОВ- равнобедренный(АО=ОВ=r), значит ∠ОАВ=∠АВО=15°. Тогда ∠ОВС =56°-15°=41°.
2) ∆ ВОС- равнобедренный(ВО=ОС=r), значит ∠ОВС=∠ВСО=41°.
8. ∆ АОВ =∆ СОD (AO=OD=r, CO=OB=r, ∠AОВ =∠CОD-вертикальные ), значит ∠ОАВ =∠ОСD=25°
...
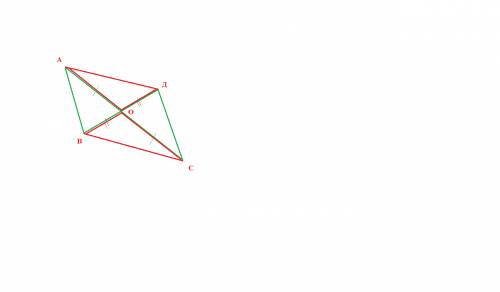
обозначим точку пересечения отрезков О
углы АОВ , ДОС - вернтикальные - равны
стороны АО, ОС равны -половины отрезка АС
стороны ВО, ОД равны -половины отрезка ВД
ПЕРВЫЙ признак равенства :
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
треугольники АОВ , ДОС - РАВНЫ
тоже самое с треугольниками АОД и ВОС - тоже равны - по тому же признаку
теперь
треугольник АВС = треуг АОВ +треуг ВОС
треугольник СДА = треуг АОД +треуг ДОС
треугольники АВС и СДА равны, потому что состоят из двух равных треуг-ков
ДОКАЗАНО
Объяснение:
В рівнобедреному прямокутному трикутнику основою є гіпотенуза.
За теоремою Піфагору с²=2а² (тому що а=в)
10²=2а²
100:2=а²
50=а²
а=√50=5√2 см