Основи рівнобічної трапеції дорівнюють 22 см і 12 см,а бічна сторона-13 см.знайтивисоту трапеції.

👇

Ответ:

romamrn

07.05.2022

1. ВН и СН1 - высоты трапеции.
2. ВНН1С-прямоугольник, ВС=НН1=12
3. АД=22 по условию, трапеция равнобокая, значит, АН=Н1С=(22-12):2=5
4. Треугольник АВН-прямоугольный, по т. Пифагора ВН²=АВ²-АН²=13²=-5²=169-25=144
ВН=√144=12

4,7(92 оценок)

Открыть все ответы

Ответ:

viakobchuk

07.05.2022

ответ:

Что и требовалось доказать!

Объяснение:

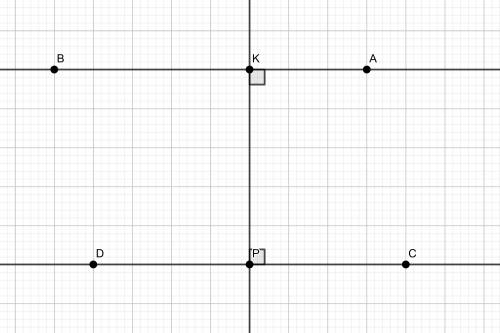
Теорема: "Если при пересечении двух прямых секущей односторонние углы в сумме составляют 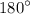${180}^{\circ}$ , то прямые параллельны".

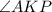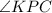$\angle AKP$ и $\angle KPC$ - односторонние при пересечении прямых 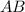и 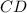секущей .

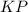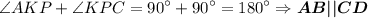$\angle AKP + \angle KPC = {90}^{\circ}+{90}^{\circ}={180}^{\circ}\Rightarrow \boldsymbol{AB||CD}$ .

Что и требовалось доказать!

- - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

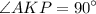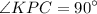
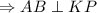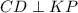Т.к. $\angle AKP={90}^{\circ}$ и $\angle KPC={90}^{\circ}$ $\Rightarrow AB \perp KP$ и $CD\perp KP$ .

Признак: "Если две различные прямые на плоскости перпендикулярны к одной и той же прямой, то они параллельны".

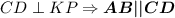Т.к. $AB\perp KP$ и $CD \perp KP \Rightarrow \boldsymbol{AB||CD}$ .

Что и требовалось доказать!

- - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

1. прямая kp пересекает прямую ав в точке к, а прямую cd в точке p. параллельны ли прямые ав и cd, е

4,4(54 оценок)

Ответ:

mruzer1999

07.05.2022

Я решила так.
1. Правильный пятиугольник, сторона = 1 см.
Отношение диагонали правильного пятиугольника к стороне = золотому сечению (то есть числу (1+√5)÷2).
Считаем: х÷1 = (1+√5)÷2
x = 1.6180339888 (см)

2.Правильный шестиугольник, сторона = 5 см.
При проведении меньшей диагонали получаем треугольник, у которого тупой угол = 120°, острые углы = по 30° каждый.

Решение 1. Меньшая диагональ правильного шестиугольника в √3 раз больше его стороны (это - свойство правильного шестиугольника), то есть = 5×√3 = 8.6602540378 (см).

Решение 2. Основано на правиле о том, что катет, лежащий против угла в 30°, равен половине гипотенузы. Нарисуй, и сразу все увидишь!
Если провести в правильном шестиугольнике и меньшую, и большую диагонали, то большая диагональ является гипотенузой прямоугольного треугольника, а меньшая диагональ является одним из катетов.
Получается, что нам именно и известен этот самый катет, лежащий напротив угла в 30°, он = 5 см. Тогда гипотенуза - она же большая диагональ, = 10 см. Остаётся по Пифагору найти второй катет (он же меньшая диагональ), х² = 10²-5²; х = √75 = 8.6602540378 (см).

4,5(20 оценок)

Это интересно:

Образование-и-коммуникации

26.01.2022

Как написать сочинение Как я провел лето : советы и рекомендации...

Компьютеры-и-электроника

18.01.2021

Как правильно пинговать IP адрес: простой гайд для начинающих...

Финансы-и-бизнес

21.12.2022

Как выбрать и купить восстановленный деревянный стол...

Здоровье