Каждое основание n-угольной призмы имеет n сторон.
Ребра снования, общие с боковыми гранями, параллельны друг другу ( лежат в параллельных плоскостях) и составляют n пар двугранных углов - по одному при верхнем и нижнем основании. . Сумма этих углов при каждой грани равна сумме линейных углов при ребрах верхнего и нижнего основания.
Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
Сумма углов, образующихся при этом у каждого ребра основания, равна сумме внутренних углов, образующихся при пересечении параллельных прямых секущей, т.е. 180°.
Следовательно, сумма двугранных углов, прилежащих к ребрам обоих оснований, равна n•180°
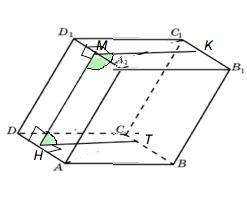
Для примера рассмотрим четырехугольную призму АВСDD1А1В1С1
Сумма двугранных углов КМН+ТНМ = 180°,
а сумма всех двугранных углов 4-угольной призмы равна 180•4=720°
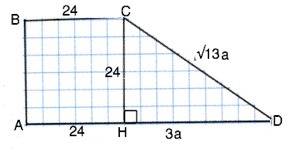
Пусть данная трапеция АВСD, отрезок СН – её высота. Так как АВСD прямоугольная трапеция, ВА⊥АD и СН⊥АD. ⇒ АВ=СН. По условию ВС=СН, ⇒ АВСН - квадрат. АН=ВС=СН=24. Косинус угла есть отношение катета, прилежащего углу, к гипотенузе. cos∠D=HD:CD
Примем коэффициент отношения НD:СD равным а. Тогда НD=3а, СD=а√13. Из прямоугольного ∆ СНD по т.Пифагора СН²=СD²-НD² 576=13а²-9а² ⇒ а=12, а НD=3а=36. Большее основание АD=AH+HD=24+36=60 (ед. длины).
Или:
СD=СН:sin∠D. Из основного тригонометрического тождества sin∠D=√(1-cos*D)=√(1-9/13)=2/√13 Гипотенуза СD=24:(2/√13)=12√13, откуда HD=CD•cos∠D=12√13•3:√13=36. Основание АD=24+36=60 (ед. длины)
Так как у ромба углы делятся диагоналями то острые углы в образовавшихся прямоугольных треугольниках будут равны 30 градусов. А по свойству прямоугольно треугольника катет лежащий напротив угла 30 градусов равен половине гипотенузы. Гипотенуза у нас сторона ромба.
Найдем этот катет 1/2 35 = 17.5 первый катет и соответственно одна из полу диагоналей.
17.5*2 = 35 см будет полная диагональ, одну нашли.
Найдем вторую через значение первого катета
По теореме пифагора
35^2-17.5^2=918.75 под корнем
это полу диагональ, найдем целиком диагональ
918.75 под корнем * 2 = 2 под корнем 918.75
Какая же диагональ будет наименьшей? тут и так понятно но можно посчитать возведя числа в квадрат
35^2=1225
2 под корнем 918.75 все в квадрате равно = 4*918.75 = 3675.
Значит наименьшая диагональ равна 35 см.