Картинка в этой задаче действительно желательна.
Объем правильной треугольной призмы равен произведению площади основания на высоту призмы.
Площадь основания - это площадь правильного треугольника со стороной а.
Формула площади равностороннего треугольника
S=(a²√3):4
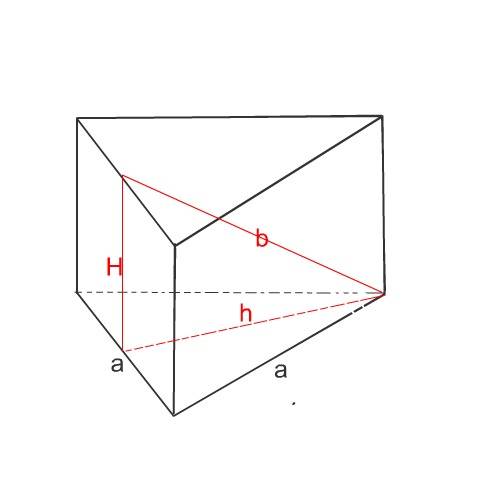
Высоту призмы найдем из прямоугольного треугольника,
катеты в котором- высота призмы и высота треугольника=основания,
а гипотенуза - данное в условии расстояние b от вершины одного основания до противолежащей стороны другого основания.
Высота правильного треугольника находится по формуле
h=а√3):2
Высоту призмы найдем по теореме Пифагора:
Н= √(b²-h²)=√(b²-3а²:4)
V= (a²√3):4)·√(b²-3а²:4)
пусть ABC - прямоугольный треугольник с прямым углом B=90 градусов
Тогда гипотенуза АС=17 см.
ПУсть нам медина выходит из точки А(выбор вершины с которой опущена медиана на катет не влияет на задачу)
Пусть АM - медиана(тогда BM=CM)
Обозначим катет BC через y, AC через x, тогда BM=CM=y\2,по теореме Пифагора
получаем систему и з двух уравнений
первое х^2+y^2=17^2
второе x^2+(y\2)^2=15^2
Отняв от первое второе получаем 3\4*(y^2)=64
y^2=256\3
y=(+\-)16\корень(3)=(+\-)16\3*корень(3)
нас удовлетворяет только положительный корень(длина катета не может быть отрицательным числом), так что y=16\3*корень(3)
подставив найденное значение y в первое уравнение находим х
х^2+y^2=17^2
х^2+256\3=17^2
х^2=611\3
х=(+\-)корень(611\3)
(нас удовлетворяет только положительное значение по той же причине что и выше)
х=корень(611\3)
ответ корень(611\3) и 16\3*корень(3) катеты треугольника
30*2=60 - периметр большего треугольника
4х - первая стор.треугольника
5х - вторая стор.треугольника
6х - третья стор.треугольника
Составим уравнение:
4х+5х+6х=60
15х=60
х=4
4*4=16 - первая сторона 16:2=8 средн.линия первой стороны
4*5=20 - вторая сторона 20:2=10 - средняя линия второй стороны
4*6=24 - третья сторона 24:2=12 - средняя линия третьей стороны