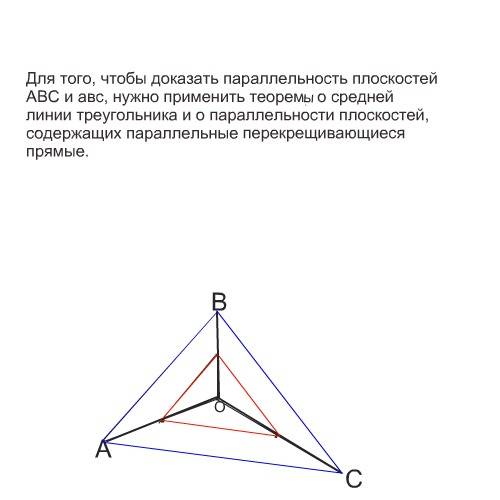
Сделайте рисунок к задаче. Он может выглядеть как угол комнаты - отрезки направлены в разные стороны.
Соедините концы отрезков А, В и С и проведите через них плоскость ( Через любые три точки пространства, не лежащие на одной прямой, можно провести одну и только одну плоскость.)
Обратите внимание на то, что при соединении свободных концов отрезков получились три треугольника:АОВ, ВОС и АОС.
Отрезки прямых, соединяющие середины сторон АО, ВО и ВС, соответственно параллельны сторонам АВ, ВС и АС как средние линии треугольников АОВ, ВОС и АОС. Проведенная через середины отрезков плоскость будет параллельна плоскости АВС :Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Что и требовалось доказать.
ответ:площадь ромба равна 72√3 см2
Объяснение: В условии нам задан ромб со стороной 12 см и острым углом 60°. Для того, чтобы найти площадь ромба давайте вспомним формулу для нахождения площади через сторону ромба и угол между ними.
Итак, формула нахождения площади выглядит так:
S = a2 * sin a.
Площадь ромба равна произведению сторон на синус угла между ними.
Нам известны стороны ромба и угол между ними. Остается только подставить и произвести вычисления:
S = a2 * sin a = 122 * Sin 60° = 144 * √3/2 = 72√3 см2.