а) Проекция точки S на плоскость основания это точка O — центр основания. Центр правильного треугольника является точкой пересечения его медиан, поэтому . Прямая проецируется на плоскость основания и прямую Поэтому проекция точки — точка — лежит на отрезке M — середина AS, поэтому ее проекция — это середина отрезка AO. Таким образом, проекции точек S и M на плоскость основания делят высоту AN треугольника ABC на три равные части.
б) Прямая проектируется на плоскость основания в прямую Поэтому проекция точки — точка — лежит на отрезке Значит, прямая является проекцией прямой следовательно, угол — искомый. Заметим, что где — центр основания, значит, — средняя линия треугольника а поэтому — середина
Тогда
и
Из прямоугольного треугольника находим:
Из прямоугольного треугольника находим:
Значит, искомый угол равен
ответ:arctg 10/21
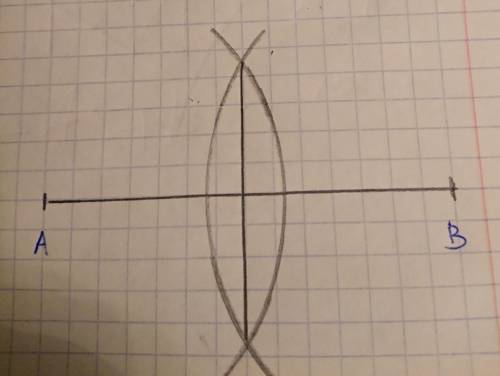
См. рисунок и объяснения.
Объяснение:
В данном случае предпологается, что линейка без делений. Т.е. просто инструмент для проведения линий.
Берём циркуль и выставляем ножки циркуля на расстояние чуть боьше середины отрезка (примерно 1-2 см). Проводим окружность с центром в одном конце отрезка и другую окружность с центром в другом конце отрезка.
Поскольку окружности одинаковые, то пересечения будут симметричные.
Дальше линейкой соединяем точки пересечения окружностей. Полученный отрезок будет перпендикуляерн первоначальному и бедут делить его пополам.