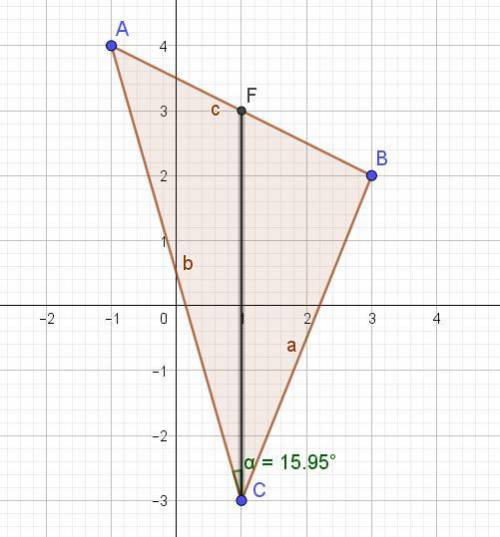
Найдем координату точки F. F- точка , которая делит пополам сторону АВ ( так как CF - медиана).
F = ( (Xa+Xb)/2 ; (Ya+Yb)/2) = ((-1+3)/2 ; (4+2)/2)= (1;3).
Вектор CF = (1-1; 3-(-3)) = (0; 6).
Уравнение медианы CF: (x - 1)/0 = (y - 4)/6.
Получаем общее уравнение CF: 6x - 6 = 0 или х - 1 = 0.
Находим уравнение стороны АС.
Вектор АС = (1-(-1); -3-4) = (2; -7).
Уравнение АС: (x + 1)/2 = (y - 4)/(-7) или в общем виде 7x + 2y - 1 = 0.
Находим угол α между прямыми АС и CF.
cos α = (1*7 + 0*2)/(1*√53) = 7√53/53.
Угол α = 15,9454°.
ответ: ∡ACF=arccos(3*√5/10)
Объяснение:
1. Найдем координату точки F. F- точка , которая делит пополам сторону АВ ( так как CF - медиана)
F = ( (Xa+Xb)/2 ; (Ya+Yb)/2) = ((-1+3)/2 ; (4+2)/2)= (1;3)
2. Найдем длину медианы CF:
CF=sqrt( (Xf-Xc)²+(Yf-Yc)²)= sqrt((1-1)²+ (3-(-3))²)=sqrt(0+9)=3
3. Найдем AF =sqrt ((Xf-Xa)² +(Yf-Ya)²)= sqrt ((1-(-1))²+(3-4)²)= sqrt(2²+1²)=√5
4. Найдем АС=sqrt((Xc-Xa)²+(Yc-Ya)²)=sqrt((1-(-1))²+(-3-(-4))²)=sqrt(2²+1²)=√5
=> ΔACF- равнобедренный (AС=AF).
=>cos ∡ACF= 3/√5/2=3*√5/10
∡ACF=arccos(3*√5/10)
В параллелограмме <B=180°-<A (так как углы параллелограмма, прилежащие к одной стороне, в сумме равны 180°. Cos(180-α)=-Cosα (формула).
По теореме косинусов:
ВD²=АВ²+АD²-2*АВ*АD*CosA. Или ВD²=338-238*CosA.
АС²=АВ²+АD²+2*АВ*АD*CosA. Или АС²=338+238*CosA.
В прямоугольном треугольнике АСС1 угол САС1 при основании равен 30°(дано).
Тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть СС1/АС=√3/3, а СС1=АС*√3/3.
В прямоугольном треугольнике BDB1 угол BDB1 при основании равен 45°(дано).
Значит BB1=BD. ВВ1=СС1 = Н (высота параллелепипеда).
Н²=BD² (1)
H²=AC²(√3/3)²=АС²(1/3) (2).
Приравняем (1) и (2):
338-238*CosA=(1/3)(338+238*CosA). Отсюда
1014-714CosA=338+238CosA и CosA=676/952=169/238.
Тогда из (1) имеем: Н=√(338-238*169/238)=√(338-169=13см.
ответ: высота параллелепипеда равна 13см.