Шел длинным путем. Доказал. И задумался. А зачем условие равнобедренности?)
.
а) ∠DВМ=∠МВС; по условию, ∠МВС=∠ВМD, как внутр. накрест лежащие при DМ║ВС и секущей ВМ, Мзанчит, ДМ=ВD.
б) ∠МСD=∠ВСD по условию; ∠DСВ=∠СМ, как внутр. накрест лежащие при DМ║ВС и секущей DС, занчит, DМ=МС.
из а) и б)⇒DМ=ВD=МС
как бы обошелся без того, что треугольник равнобедренный.
Положим, что равные углы, а именно ∠МВС=∠DСВ=α
как половины равных углов при основании равнобедренного треугольника .
а т.к. в ΔВМС ∠В+∠С=α+2α=3α, то ∠ВМС=180°-3α; т.к. ДМ║ВС, то ∠DМС+∠ВСМ=180°⇒∠ВМD=180°-(180-3α)-2α=α⇒DМ=ВD; и опять таки т.к. DМ║ВС при секущей DС : ∠СDМ=∠DСВ. как внутр. накрест лежащие , т.е. тоже равен α⇒ DМ=МС
а из того, что ВD= DМ и МС=DМ⇒DМ=ВD=МС Доказано. но не покидает ощущение недосказанности. если можно доказать равенство не прибегая к равнобедренности треугольника, то зачем это лишнее условие?)
<А=<С=120°, <В<Д=60°
Объяснение:
обозначим вершины ромба А В С Д с диагоналями АС и ВД а точку их пересечения О. Диагонали ромба пересекаясь делятся пополам под прямым углом, образуя 4 равных прямоугольных треугольника, а также противоположные углы ромба равны и диагонали при пересечении делят углы из которых они проведены, пополам, поэтому АО=СО=2÷2=1см, ВО=ДО=2√3÷2=√3см
Теперь найдём угол через тангенс угла АВО. Тангенс угла - это отношение противолежащего от
угла катета к прилежащему:
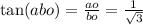
tg 1/√3=30°- это половина угла В,
Тогда <В=<Д=30×2=60°
Сумма углов ромба, прилегающие к одной стороне, составляет 180°, поэтому <А=<С=180–60=120°
обращаю внимание что 1/√3=√3/3, поскольку 1/√3 - это сокращённая дробь от √3/3. В тригонометрической таблице указано именно √3/3
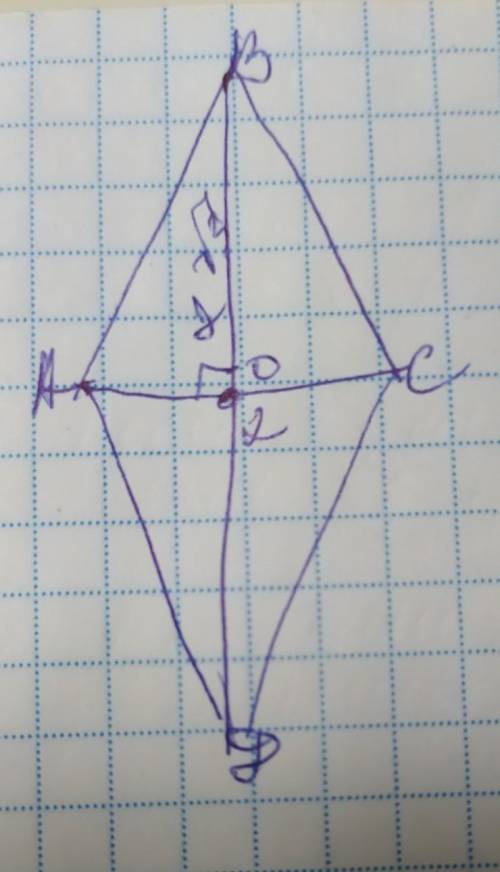
пусть ромб будет АВСД
ВО=ОД АО=ОС ( диагонали)
ВО равно и перпендикулярно ОД=20 АО равно и перпендикулярно ОС=15
АВО - прямоугольный
АВ2=АО2+ВО2=400=225=625
АВ=25
АО*ОВ=rАВ
r=300:25=12 см