ΔDCF= ΔADF ( по катету и гипотенузе) .
Значит, FD= 12.
4) Из Δ FDC- прям.: FC² +CD²=FD²
Пусть СD=BC=FB= x, тогда ( x√2)²+x²=12²
2x²+x²=144
3x²=144
x²=48
x=√48=4√3(cм)
FC= 4√3 cм = высота.
б) Площадь боковой поверхности пирамиды равна сумме площадей боковых граней, а о том , что представляют собой грани сказано выше. Стоит отметить , что равные фигуры имеют равные площади, тогда
S =2·S abf + 2·S cdf = 2·( ½·AB·BF+½·CD·CF)= 4√3·4√3 +4√3·4√6= 48 +16√18=
= 48 +48√2 =48·(1+√2) cм².
![Если можно,с рисунком : ] 1) основанием пирамиды является квадрат,одно из боковых ребер перепендикул](/tpl/images/0012/8962/e18de.jpg)
2)
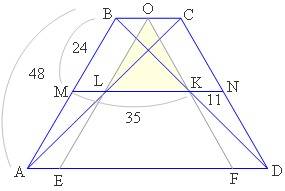
Проведём ОЕ и ОF параллельно боковым сторонам через точки пересечения средней линии трапеции с её диагоналями.
ОЕ и ОF пересекутся в точке О на основании ВС, так как находятся на расстоянии 11см от боковых сторон,
а верхнее основание ВС=22см. (Это легко вычислить, используя подобие тр. МВК и АВD)
Получившийся треугольник LOK равносторонний (каждая сторона равна 24см) и, следовательно, его углы равны по 60град.
Отсюда ясно, что углы трапеции при большем основании также равны по 60град. (соответственные углы при параллельных прямых).
Углы трапеции при верхнем основании равны по 180-60=120град.