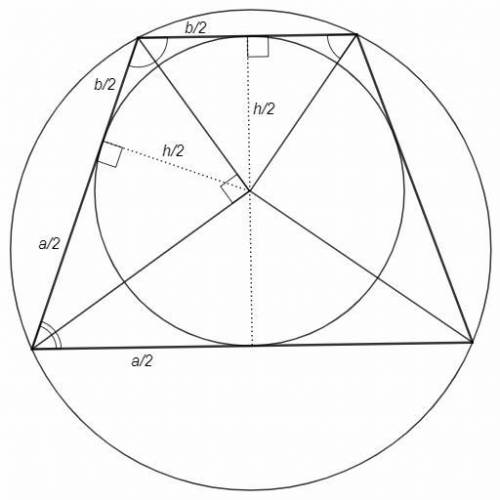
Трапеция описанная, следовательно её биссектрисы пересекаются в одной точке (центр вписанной окружности). Трапеция вписанная, следовательно равнобедренная, углы при основании равны. Значит равны их половины, биссектрисы углов при основании образуют равнобедренный треугольник. Перпендикуляр из центра вписанной окружности к основанию (радиус) является медианой.
Биссектрисы внутренних углов при параллельных пересекаются под прямым углом. Радиус в точку касания на боковой стороне - высота из прямого угла, она равна среднему пропорциональному проекций катетов. Отрезки касательных из одной точки равны, проекции катетов равны половинам оснований. Радиус равен половине высоты. Таким образом h=√(ab)
S= а·H или S= b·h,
где H- высота, проведённая к стороне а, h- высота, проведенная к стороне b
Р=2(а+b)
28=2(а+b)
a+b=14, b=14-а
В равенство
а·H=b·h
данные
а·3=(14-а)·4 или а·4=(14-а)·3
3а=56-4а или 4а=42-3а
7а=56 или 7а=42
а=8 или а=6
тогда
b=14-8 b=14-6
b=6 b=8
ответы получились симметричные, поэтому один вариант. Одна сторона параллелограмма 6 см, другая 8 см