Вугол с величиной 19 градусов вписана окружность, которая касается сторон угла в точках а и в. найдите угол аов. ответ дайте в градусах. в параллелограмме abcd диагональ ас в 2 раза больше стороны ав и уголacd=154.найдите угол между диагоналями параллелограмма.ответ дайте в градусах

👇

Ответ:

dianochka471

20.03.2020

Первая задача. Смотри рисунок.
360-90-90-19=161.
ответ: 161.

Вторая задача. Смотри рисунок.
Пусть О - точка пересечения диагоналей. Она делит эти диагонали пополам, значит
СО=АО. Из условия задачи можно заключить, что СО=СД. Тогда ΔСДО - равнобедренный и угол СОД=углуСДО=(180-154)/2=13.
Значит угол СОД, находящийся между диагоналями равен 13. Но у нас также есть еще один угол между диагоналями, например, ДОА, который равен 180-13=167.
ответ: 13, 167.

4,6(18 оценок)

Открыть все ответы

Ответ:

AlexMYP

20.03.2020

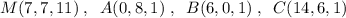
$M(7,7,11)\; ,\; \; A(0,8,1)\; ,\; \; B(6,0,1)\; ,\; \; C(14,6,1)$

1) Высота правильной пирамиды проходит через СЕРЕДИНУ её основания. Основанием правильной четырёхугольной ПИРАМИДЫ служит КВАДРАТ. Его центр совпадает с точкой пересечения ДИАГОНАЛЕЙ, которая является СЕРЕДИНОЙ каждой из диагоналей квадрата.

Найдём координаты точки Н - середины ДИАГОНАЛИ АС:

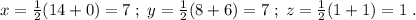
$x=\frac{1}{2}(14+0)=7\; ;\; y=\frac{1}{2}(8+6)=7\; ;\; z=\frac{1}{2}(1+1)=1\; .$

Итак, Н(7,7,1) .

Вычислим высоту МН пирамиды:

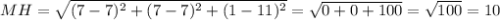
$MH=\sqrt{(7-7)^2+(7-7)^2+(1-11)^2}=\sqrt{0+0+100}=\sqrt{100}=10$

2) Апофема правильной пирамиды - это отрезок, соединяющий ВЕРШИНУ пирамиды с СЕРЕДИНОЙ стороны основания. Найдём координаты точки Р - середины СТОРОНЫ основания АВ:

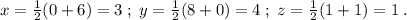
$x=\frac{1}{2}(0+6)=3\; ;\; y=\frac{1}{2}(8+0)=4\; ;\; z=\frac{1}{2}(1+1)=1\; .$

Итак, Р(3,4,1) . Следовательно,

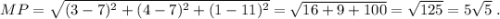
$MP=\sqrt{(3-7)^2+(4-7)^2+(1-11)^2}=\sqrt{16+9+100}=\sqrt{125}=5\sqrt5\; .$

3) Площадь боковой поверхности правильной пирамиды равна ПОЛОВИНЕ произведения ПЕРИМЕТРА основания и апофемы пирамиды. Найдём сторону АВ - СТОРОНУ ОСНОВАНИЯ пирамиды:

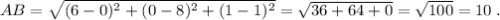
$AB=\sqrt{(6-0)^2+(0-8)^2+(1-1)^2}=\sqrt{36+64+0}=\sqrt{100}=10\; .$

ВЫЧИСЛИМ ПЕРИМЕТР ПИРАМИДЫ: 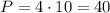$P=4\cdot 10=40$ .

Вычислим площадь боковой поверхности пирамиды:

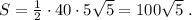
$S=\frac{1}{2}\cdot 40\cdot 5\sqrt5=100\sqrt5\; .$

4,4(49 оценок)

Ответ:

Katiadimova3

20.03.2020

По первому признаку подобия треугольников имеем, что данные равнобедр.треуг. подобны. Коэффициент их подобия равен как отношению соотв.сторон, так и отношению периметров. Найдем боковые стороны первого треугольника. Высота к основанию является также медианой, значит по теореме Пифагора боковая сторона равна кореньиз(64+36)=10. Периметр первого треугольника равен 10+10+16=36. Коэффициент подобия k=54/36=3/2=1,5. Значит боковые стороны второго равнобедр.треугольника равны 10*1,5=15 см, а основание равно 16*1,5=24 см.

4,8(22 оценок)

Это интересно:

Кулинария-и-гостеприимство

11.11.2022

Сладкий рецепт: американские панкейки с нутеллой...

Кулинария-и-гостеприимство

04.04.2021

Как готовить только для себя: полезные советы и рецепты...

Дом-и-сад

23.11.2020

Как навести порядок в гараже: полезные советы от специалистов...

Транспорт